
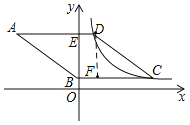
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

【答案】![]()
【解析】
过点D作DF⊥BC于点F,由菱形的性质可得BC=CD,AD∥BC,可证四边形DEBF是矩形,可得DF=BE,DE=BF,在Rt△DFC中,由勾股定理可求DE=1,DF=3,由反比例函数的性质可求k的值.
如图,过点D作DF⊥BC于点F,
∵四边形ABCD是菱形,
∴BC=CD,AD∥BC,
∵∠DEB=90°,AD∥BC,
∴∠EBC=90°,且∠DEB=90°,DF⊥BC,
∴四边形DEBF是矩形,
∴DF=BE,DE=BF,
∵点C的横坐标为5,BE=3DE,
∴BC=CD=5,DF=3DE,CF=5﹣DE,
∵CD2=DF2+CF2,
∴25=9DE2+(5﹣DE)2,
∴DE=1,
∴DF=BE=3,
设点C(5,m),点D(1,m+3),
∵反比例函数y=![]() 图象过点C,D,
图象过点C,D,
∴5m=1×(m+3),
∴m=![]() ,
,
∴点C(5,![]() ),
),
∴k=5×![]() =
=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
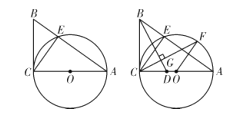
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
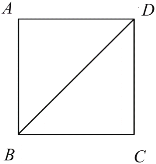
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 是正方形所在平面内一动点,满足
是正方形所在平面内一动点,满足![]() .
.
(1)当点![]() 在直线
在直线![]() 上方且
上方且![]() 时,求证:
时,求证:![]() ;
;
(2)若![]() ,求点
,求点![]() 到直线
到直线![]() 的距离;
的距离;
(3)记![]() ,在点
,在点![]() 运动过程中,
运动过程中,![]() 是否存在最大值或最小值?若存在,求出其值,若不存在,说明理由.
是否存在最大值或最小值?若存在,求出其值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠肺炎”肆虐时,无数抗疫英雄涌现,七年级(2)班老师为让同学们更深人地了解抗疫英雄钟南山、李兰娟、李文亮、张文宏(依次记为A、B、C、D)的事迹,设计了如下活动:取四张完全相同的卡片.分别写上A、B、C、D)四个标号,然后背面朝上放置在水平桌面上,搅匀后每个同学从中随机抽取一张卡片,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相对应抗疫英雄的资料,并做成小报.
(1)求小欢同学抽到的卡片上是钟南山的概率;
(2)请用列表法或画树状图的方法,求小平和小安两位同学抽到的卡片上是不同英雄的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=![]() (即tan∠DEM=
(即tan∠DEM=![]() ),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号).
),且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上,求条幅AB的长度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 与
与![]() 相交于点E,连接CE.
相交于点E,连接CE.
(1)求证:![]() ;
;
(2)如果![]() 的面积为3,求
的面积为3,求![]() 的面积;
的面积;
(3)如![]() 图的角平分线BD交AC于点D,
图的角平分线BD交AC于点D,![]() 于点
于点![]() 交
交![]() 于点F,连接
于点F,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com