
【题目】甲、乙两人参加某体育训练项目,近期的五次测试成绩得分情况如图.
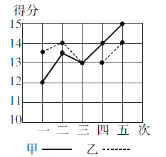
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
【答案】(1)甲的平均数为13.5分,方差为1;乙的平均数为13.5分,方差为0.2;(2) 乙的成绩较稳定,但甲的潜力大.
【解析】
(1)由折线图列出甲、乙近期的五次测试成绩得分,由此能求出两人得分的平均数与方差.(2)甲、乙二人的平均成绩相等,但乙比甲的成绩更稳定.
解:(1)解:(Ⅰ)由折线图知甲近期的五次测试成绩得分分别为:12,13.5,13,14,15,
∴甲得分的平均数为:![]() =
=![]() (12+13.5+13+14+15)=13.5.
(12+13.5+13+14+15)=13.5.
方差为:S12=![]() [(12-13.5)2+(13.5-13.5)2+(13-13.5)2+(14-13.5)2+(15-13.5)2]=1
[(12-13.5)2+(13.5-13.5)2+(13-13.5)2+(14-13.5)2+(15-13.5)2]=1
乙近期的五次测试成绩得分分别为:13.5, 14,13,13,14.
∴乙得分的平均数为:![]() =
=![]() (13.5+14+13+13+14)=13.5.
(13.5+14+13+13+14)=13.5.
方差为:S22=![]() [(13.5-13.5)2+(14-13.5)2+(13-13.5)2+(13-13.5)2+(14-13.5)2]= 0.2.
[(13.5-13.5)2+(14-13.5)2+(13-13.5)2+(13-13.5)2+(14-13.5)2]= 0.2.
甲的平均数为13.5分,方差为1;乙的平均数为13.5分,方差为0.2.
(2)∵![]() =
=![]() ,S12> S22
,S12> S22
∴甲、乙二人的平均成绩相等,乙的成绩较稳定,但甲的潜力大.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( ) 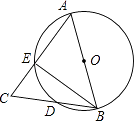
A.22.5°
B.23°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= ![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).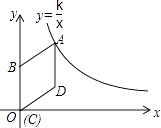
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y= ![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,边长为2的正方形ABCD中,点P在AB边上(不与点A、B重合),点Q在BC边上(不与点B、C重合)
第一次操作:将线段PQ绕点Q顺时针旋转,当点P落在正方形上时,记为点M;
第二次操作:将线段QM绕点M顺时针旋转,当点Q落在正方形上时,记为点N;
依次操作下去…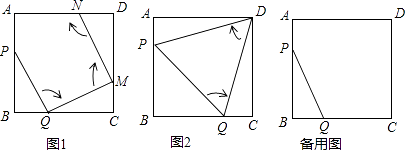
(1)如图2,经过两次操作后得到△PQD、△PQD的形状是 , 求此时线段PQ的长 ;
(2)若经过三次操作可得到四边形PQMN.
①请直接判断四边形PQMN的形状,直接写出此时此刻AP与BQ的数量关系;
②以①中的结论为前提,直接写出四边形PQMN的面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
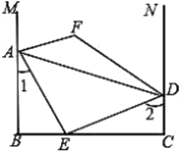
【题目】如图,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 分别是
分别是![]() 延长线上的点,
延长线上的点,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 为定值.其中结论正确的有_______(填写所有正确的序号).
为定值.其中结论正确的有_______(填写所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
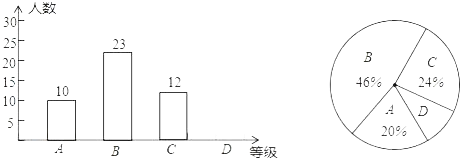
【题目】某校为了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)计算D级的学生人数,并把条形统计图补充完整;
(2)计算扇形统计图中A级所在的扇形的圆心角度数:
(3)若该校七年级有600名学生,请估计体育测试中B级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从坐标原点出发,沿x轴的正方向运动,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.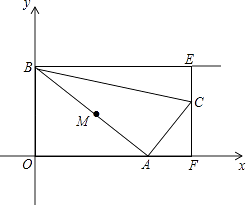
(1)当点C与点E恰好重合时,求t的值;
(2)当t为何值时,BC取得最小值;
(3)设△BCE的面积为S,当S=6时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据问题填空:
(1)问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;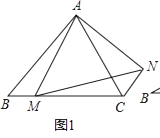
(2)深入探究:
如图②,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;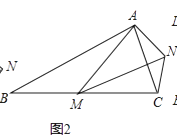
(3)拓展延伸:
如图③,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN= ![]() ,试求EF的长.
,试求EF的长.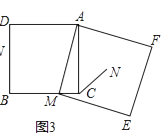
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com