
����Ŀ����ͼ����A������ԭ���������x����������˶�����B����Ϊ��0��4����M���߶�AB���е㣬����M�Ƶ�A˳ʱ�뷽����ת90��õ���C������C��x��Ĵ��ߣ�����ΪF������B��y��Ĵ�����ֱ��CF�ཻ�ڵ�E������AC��BC�����A�ĺ�����Ϊt��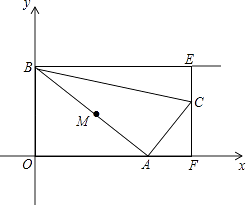
��1������C���Eǡ���غ�ʱ����t��ֵ��
��2����tΪ��ֵʱ��BCȡ����Сֵ��
��3�����BCE�����ΪS����S=6ʱ����t��ֵ��
���𰸡�
��1���⣺����C���E�غ�ʱ����ͼ1��
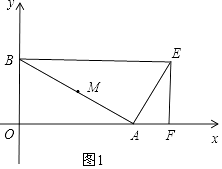
��OB=EF=4��OA=t����AB=2AE��
���������֪��BAE=90�㣬
���EAF+��BAO=��EAF+��AEF=90�㣬
���AEF=��BAO���ҡ�EFA=��AOB��
��Rt��AEF��Rt��BAO��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() �����t=8
�����t=8
��2���⣺��ͼ2��
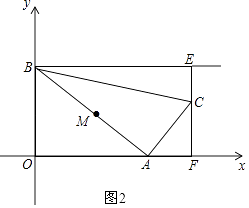
��AB=2AC��
��BC= ![]() =
= ![]() AC��
AC��
�� ![]() ��
��
��Rt��AOB�У��ɹ��ɶ����ɵ� ![]() ��
��
�൱t=0ʱ��AB����С����BC����Сֵ
��3���⣺�ٵ�0��t��8ʱ�����C�ڵ�E���·�����ͼ2��
ͬ��1����֪ ![]() =
= ![]() =
= ![]() �����AF=2��CF=
�����AF=2��CF= ![]() t��
t��
��BE=OF=OA+AF=t+2��CE=EF��CF=4�� ![]() t��
t��
��S= ![]() BECE=
BECE= ![]() ��t+2����4��
��t+2����4�� ![]() t��=��
t��=�� ![]() t2+
t2+ ![]() t+4��
t+4��
��S=6���ɵé� ![]() t2+
t2+ ![]() t+4=6�����t=2��t=4��
t+4=6�����t=2��t=4��
�ڵ�t��8ʱ�����C�ڵ�E���Ϸ�����ͼ3��
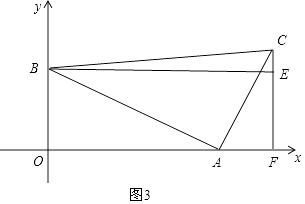
��CE=CF��EF= ![]() t��4��
t��4��
��S= ![]() BECE=
BECE= ![]() ��t+2����
��t+2���� ![]() t��4��=
t��4��= ![]() t2��
t2�� ![]() t��4��
t��4��
��S=6�ɵ� ![]() t2��
t2�� ![]() t��4=6�����t=��4����ȥ����t=10��
t��4=6�����t=��4����ȥ����t=10��
����S��ֵΪ6ʱ��t��ֵΪ2��4��10
����������1������֤����AEF�ס�BAO��Ȼ���������������ζ�Ӧ�߳ɱ����������з�����⼴�ɣ�
��2����Rt��ABC�п����BC��AB�Ĺ�ϵ��Ȼ����Rt��AOB�У���t�ɱ�ʾ��AB��Ȼ���ٿ���t��ʾ��BC��������ö��κ��������ʿ����BCȡ����Сֵʱt��ֵ��
��3����Ϊ0��t��8��t��8����������S����t�ĺ�������ʽ���������S=6���Ӷ��ɵõ�����t�ķ��̣��Ӷ������t��ֵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
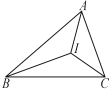
����Ŀ����ͼ������ABC�У���A��70�㣬��ABC����ACB��ƽ�����ཻ�ڵ�I�����BIC��_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˲μ�ij����ѵ����Ŀ�����ڵ���β��Գɼ��÷������ͼ��
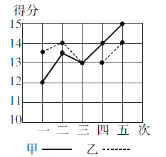
��1���ֱ�������˵÷ֵ�ƽ�����뷽�
��2������ͼ��������õĽ���������˵�ѵ���ɼ��������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η��̣�m��2��2x2+��2m+1��x+1=0����������ȵ�ʵ��������m��ȡֵ��Χ�ǣ� ��
A.m�� ![]()
B.m�� ![]() ��m��2
��m��2
C.m�� ![]()
D.m�� ![]() ��m��2
��m��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6��B����������A����һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶�������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�����1�����˶�ʱ��Ϊt��t��0���룬�����ϵ�B��ʾ�������� ������P��ʾ�������� �����ú�t�Ĵ���ʽ��ʾ������2������P��Qͬʱ�������ٵ���P�˶�������ʱ����P���Q�������ڵ���P�˶�������ʱ����P���Q��ľ���Ϊ8����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ��߾���ԭ�㣬���߷ֱ�ƽ���������ᣬ��C�ڷ���������y= ![]() ��ͼ���ϣ�����A������Ϊ����2����3������k��ֵΪ ��
��ͼ���ϣ�����A������Ϊ����2����3������k��ֵΪ �� 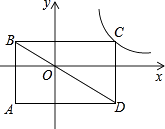
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����仭ͼ����ͼ��ֱ��CD��ֱ��AB�ཻ��C��
����������仭ͼ��

��1������P��PQ��CD����AB�ڵ�Q��
��2������P��PR��CD������ΪR��
��3������DCB=120�㣬�����PQC�Ƕ��ٶȣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB=AC�� ��1������A=36���ڡ�ABC�л�һ���߶Σ��ܵõ�2�����������Σ���������ABC������2�����������εĶ��ǵĶ����ֱ���_____����2������A��36�� ����A=_____ʱ���ڵ�����ABC�л�һ���߶Σ��ܵõ�2�����������Σ���������ABC��.��д�������𰸼��ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com