
【题目】关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )
A.m< ![]()
B.m> ![]() 且m≠2
且m≠2
C.m≤ ![]()
D.m≥ ![]() 且m≠2
且m≠2
【答案】B
【解析】解:∵关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,
∴△=b2﹣4ac>0,即(2m+1)2﹣4×(m﹣2)2×1>0,
解这个不等式得,m> ![]() ,
,
又∵二次项系数是(m﹣2)2,
∴m≠2,
故M得取值范围是m> ![]() 且m≠2.
且m≠2.
故选B.
【考点精析】掌握一元二次方程的定义和求根公式是解答本题的根本,需要知道只有一个未知数,并且未知数的项的最高系数为2的方程为一元二次方程;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 、
、![]() 上的点(点
上的点(点![]() 、
、![]() 、
、![]() 不与点
不与点![]() 重合),联结
重合),联结![]() ,交射线
,交射线![]() 与点
与点![]() .
.
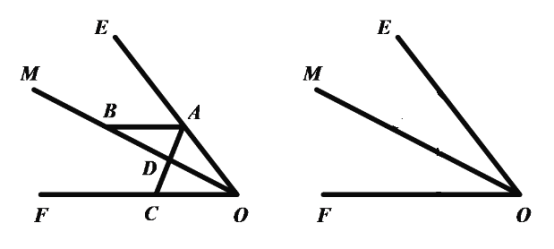
(1)如果![]() ,
,![]() 平分
平分![]() ,试判断
,试判断![]() 与射线
与射线![]() 的位置关系,试说明理由;
的位置关系,试说明理由;
(2)如果![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 中有两个相等的角,请直接写出
中有两个相等的角,请直接写出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= ![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).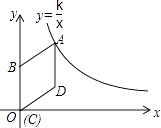
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y= ![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 分别是
分别是![]() 延长线上的点,
延长线上的点,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 为定值.其中结论正确的有_______(填写所有正确的序号).
为定值.其中结论正确的有_______(填写所有正确的序号).
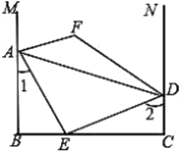
查看答案和解析>>
科目:初中数学 来源: 题型:
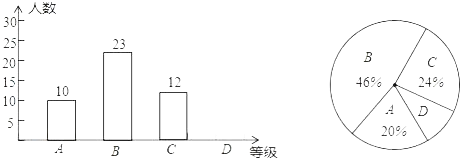
【题目】某校为了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)计算D级的学生人数,并把条形统计图补充完整;
(2)计算扇形统计图中A级所在的扇形的圆心角度数:
(3)若该校七年级有600名学生,请估计体育测试中B级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( ) 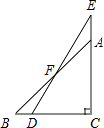
A.10°
B.15°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从坐标原点出发,沿x轴的正方向运动,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.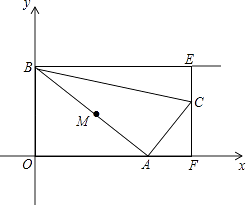
(1)当点C与点E恰好重合时,求t的值;
(2)当t为何值时,BC取得最小值;
(3)设△BCE的面积为S,当S=6时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
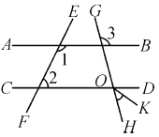
【题目】已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠KOH的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
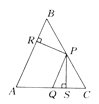
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com