
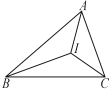
【题目】如图,在△ABC中,∠A=70°,∠ABC,∠ACB的平分线相交于点I,则∠BIC=_______________.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.
(1)去年的批发价和今年网上售价分别是多少?
(2)若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( ) 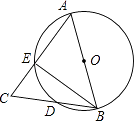
A.22.5°
B.23°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 、
、![]() 上的点(点
上的点(点![]() 、
、![]() 、
、![]() 不与点
不与点![]() 重合),联结
重合),联结![]() ,交射线
,交射线![]() 与点
与点![]() .
.
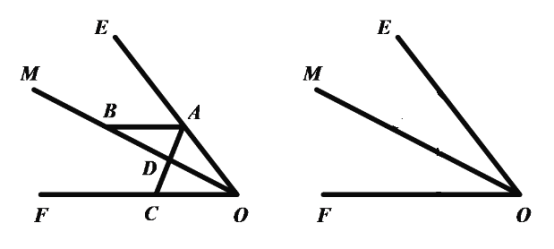
(1)如果![]() ,
,![]() 平分
平分![]() ,试判断
,试判断![]() 与射线
与射线![]() 的位置关系,试说明理由;
的位置关系,试说明理由;
(2)如果![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 中有两个相等的角,请直接写出
中有两个相等的角,请直接写出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= ![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).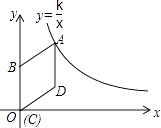
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y= ![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从坐标原点出发,沿x轴的正方向运动,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.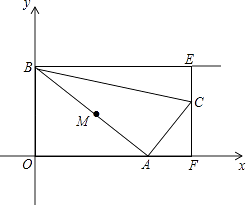
(1)当点C与点E恰好重合时,求t的值;
(2)当t为何值时,BC取得最小值;
(3)设△BCE的面积为S,当S=6时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com