
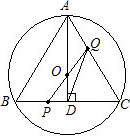
 终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).
终点C运动,速度为1cm/s;点Q沿CA向终点A运动,速度为2cm/s,设它们运动的时间为x(s).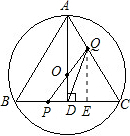 证明:(1)∵AD经过圆心,且AD⊥BC,
证明:(1)∵AD经过圆心,且AD⊥BC, PC,
PC, (4-x)
(4-x) (3)过Q作QE⊥BC于E,(如图)
(3)过Q作QE⊥BC于E,(如图) x,CE=x,
x,CE=x,
 =
= AD=
AD= 且PB=CE,BD=CD,
且PB=CE,BD=CD, QE时,PQ经过圆心
QE时,PQ经过圆心 =
=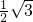 x,
x, 时,PQ⊥AC.
时,PQ⊥AC. •PD•QE=
•PD•QE= ×(2-x)×
×(2-x)× x=
x= ×(2-
×(2- )×
)× ×
× =
=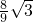 .
. PC,可得2x=
PC,可得2x= (4-x),解得x=
(4-x),解得x=
 x,CE=x,根据△ABC的边长为4,可求得AD=2
x,CE=x,根据△ABC的边长为4,可求得AD=2 ,OD=
,OD= OA=
OA= AD=
AD= 且PB=CE,BD=CD,所以PD=DE=2-x,当OD=
且PB=CE,BD=CD,所以PD=DE=2-x,当OD= QE时,PQ经过圆心,即x=
QE时,PQ经过圆心,即x= ,可求得S△PQD=
,可求得S△PQD= •PD•QE=
•PD•QE=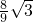 .
.

科目:初中数学 来源: 题型:
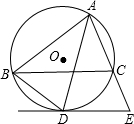 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com