
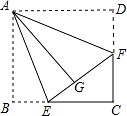
如图,正方形纸片 ABCD 的边长为 3,点 E、F 分别在边 BC、CD 上,将 AB、AD 分别和 AE、 AF 折叠,点 B、D 恰好都将在点 G 处,已知 BE=1,则 EF 的长为( )
A. 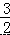 B.
B. 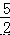 C.
C. 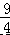 D.3
D.3
B【考点】翻折变换(折叠问题).
【专题】压轴题.
【分析】由正方形纸片 ABCD 的边长为 3,可得∠C=90°,BC=CD=3,由根据折叠的性质得:EG=BE=1, GF=DF,然后设 DF=x,在 Rt△EFC 中,由勾股定理 EF2=EC2+FC2,即可得方程,解方程即可求得 答案.
【解答】解:∵正方形纸片 ABCD 的边长为 3,
∴∠C=90°,BC=CD=3,
根据折叠的性质得:EG=BE=1,GF=DF, 设 DF=x,
则 EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2, 在 Rt△EFC 中,EF2=EC2+FC2,
即(x+1)2=22+(3﹣x)2, 解得:x= 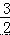 ,
,
∴DF= 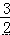 ,EF=1+
,EF=1+ 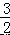 =
=  .
.
故选 B.
【点评】此题考查了折叠的性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合 思想与方程思想的应用.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线 l1 对应的函数表达式为 y=2x,直线 l2 与 x、y 轴分别交于点 A、 B,且 l1∥l2,OA=2,则线段 OB 的长为( )
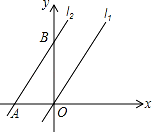
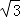 A.3 B.4 C.2
A.3 B.4 C.2 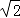 D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
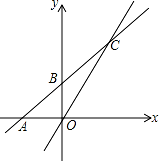
已知一次函数 y=kx+b 的图象与 x 轴交于点 A,与 y 轴交于点 B(0,2),且与正比例函数 的图象交于点 C(m,4)
(1)求 m 的值;
求一次函数 y=kx+b 的表达式;
(3)求这两个函数图象与 x 轴所围成的△AOC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
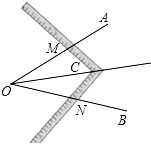
工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB 是一个任意角,在边 OA,OB 上 分别取 OM=ON,移动角尺,使角尺两边相同的刻度分别与 M,N 重合.过角尺顶点 C 作射线 OC.由 此做法得△MOC≌△NOC 的依据是( )
A.AAS B.SAS C.A SA D.SSS
SA D.SSS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com