
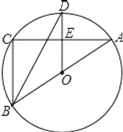
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°,BC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
科目:初中数学 来源: 题型:
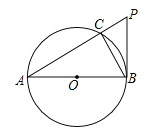
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某旅游公司国庆期间倾情打造了四条旅游路线:A.壶口瀑布,B.平遥古城,C.云冈石窟,D.五台山.
A.  B.
B.  C.
C.  D.
D. 
李老师和张老师都计划在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李老师选择线路A.壶口瀑布的概率是多少?
(2)用画树状图或列表的方法,求李老师和张老师恰好选择同一线路旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出六个函数解析式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
小明根据学习二次函数的经验,分析了上面这些函数解析式的特点,研究了它们的图象和性质。下面是小明的分析和研究过程,请补充完整:
(1)观察上面这些函数解析式,它们都具有共同的特点,可以表示为形如![]() _______,其中x为自变量;
_______,其中x为自变量;
(2)如图,在平面直角坐标系![]() 中,画出了函数
中,画出了函数![]() 的部分图象,用描点法将这个函数的图象补充完整;
的部分图象,用描点法将这个函数的图象补充完整;
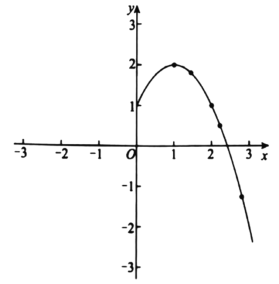
(3)对于上面这些函数,下列四个结论:
①函数图象关于y轴对称
②有些函数既有最大值,同时也有最小值
③存在某个函数,当![]() (m为正数)时,y随x的增大而增大,当
(m为正数)时,y随x的增大而增大,当![]() 时,y随x的增大而减小
时,y随x的增大而减小
④函数图象与x轴公共点的个数只可能是0个或2个或4个
所有正确结论的序号是________;
(4)结合函数图象,解决问题:若关于x的方程![]() 有一个实数根为3,则该方程其它的实数根为_______.
有一个实数根为3,则该方程其它的实数根为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象经过点
的图象经过点![]() ,且当
,且当![]() 和
和![]() 时所对应的函数值相等.一次函数
时所对应的函数值相等.一次函数![]() 与二次函数
与二次函数![]() 的图象分别交于
的图象分别交于![]() ,
, ![]() 两点,点
两点,点![]() 在第一象限.
在第一象限.

(![]() )求二次函数
)求二次函数![]() 的表达式.
的表达式.
(![]() )连接
)连接![]() ,求
,求![]() 的长.
的长.
(![]() )连接
)连接![]() ,
, ![]() 是线段
是线段![]() 得中点,将点
得中点,将点![]() 绕点
绕点![]() 旋转
旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,
, ![]() ,判断四边形
,判断四边形![]() 的性状,并证明你的结论.
的性状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
(m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
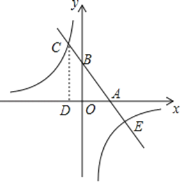
(1)求一次函数与反比例函数的解析式;
(2)求两个函数图象的另一个交点E的坐标;
(3)请观察图象,直接写出不等式kx+b≥![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张分别标有数字2,3,4,6的扑克牌,除正面的数字外,牌的形状、大小完全相同.小红先从口袋中随机摸出一张扑克牌并记下牌上的数字为x;小颖在剩下的3张扑克牌中随机摸出一张扑克牌并记下牌上的数字为y,
(1)事件①:小红摸出标有数字3的牌,事件②:小颖摸出标有数字1的牌,则( )
A.事件①是必然事件,事件②是不可能事件,
B.事件①是随机事件,事件②是不可能事件,
C.事件①是必然事件,事件②是随机事件,
D.事件①是随机事件,事件②是必然事件,
(2)若|x-y|≤2,则说明小红与小颖“心领神会”,请求出她们“心领神会”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
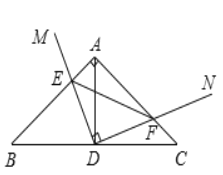
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 分别与边
分别与边![]() 、
、![]() 交于、
交于、![]() 两点.下列结论:①
两点.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 与
与![]() 可能互相平分.
可能互相平分.
其中,正确的结论是___________________(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com