【题目】如图，在平面直角坐标系中，二次函数的图象经过点，且当和时所对应的函数值相等．一次函数与二次函数的图象分别交于， 两点，点在第一象限．

（）求二次函数的表达式．

（）连接，求的长．

（）连接， 是线段得中点，将点绕点旋转得到点，连接， ，判断四边形的性状，并证明你的结论．

参考答案：

【答案】（1）；（2）；（3）见解析

【解析】（1）根据当x=0和x=5时所对应的函数值相等，可得（5，c），根据待定系数法，可得函数解析式；

（2）联立抛物线与直线，可得方程组，根据解方程组，可得B、C 的坐标根据勾股定理，可得AB的长；

（3）根据线段中点的性质，可得M点的坐标，根据旋转的性质，可得MN与BM的关系，根据平行四边形的判定，可得答案.

解：（）当时．即．

把 代入解析式．

，∴，

∴．

（）∵，∴， ．

∴， ，

∴．

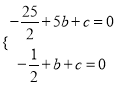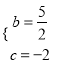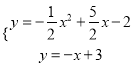（）四边形为矩形．

证：∵为中点，∴．

又∵，∴四边形为平行四边形．

又∵，∴．

在中．

．

∴，

∴四边形为矩形．

“点睛”本题考查了二次函数综合题，利用函数值相等得出（5，c）是解题关键，又利用了待定系数法求函数解析式；利用解方程组得出交点坐标，又利用了勾股定理；利用了平行四边形的判定；对角线互相平分的四边形是平行四边形.

关闭