
【题目】如图,在菱形ABCD中,∠A=60°,点E,F分别是边AB,AD上的点,且满足∠BCE=∠DCF,连结EF.

(1)若AF=1,求EF的长;
(2)取CE的中点M,连结BM,FM,BF.求证:BM⊥FM.
【答案】(1)1;(2)证明见解析.
【解析】
试题分析:(1)根据已知和菱形的性质证明△CBE≌△CDF,得到BE=DF,证明△AEF是等边三角形,求出EF的长;
(2)延长BM交DC于点N,连结FN,证明△CMN≌△EMB,得到NM=MB,证明△FDN≌△BEF,得到FN=FB,得到BM⊥MF.
试题解析:(1)∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠D=∠CBE,
又∵∠BCE=∠DCF,
在△CBE与△CDF中,
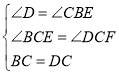 ,
,
∴△CBE≌△CDF,
∴BE=DF.
又∵AB=AD,
∴AB-BE=AD-DF,即AE=AF,
又∵∠A=60°,
∴△AEF是等边三角形,
∴EF=AF,
∵AF=1,
∴EF=1.
(2)如图1,延长BM交DC于点N,连结FN,
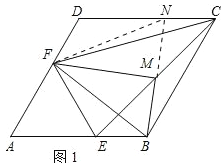
∵四边形ABCD是菱形,
∴DC∥AB,
∴∠NCM=∠BEM,∠CNM=∠EBM
∵点M是CE的中点,
∴CM=EM.
在△CMN与△EMB中,
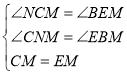 ,
,
∴△CMN≌△EMB,
∴NM=MB,CN=BE.
又∵AB=DC.
∴DC-CN=AB-BE,即DN=AE.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠BEF=120°,EF=DN.
∵DC∥AB,
∴∠A+∠D=180°,
又∵∠A=60°,
∴∠D=120°,
∴∠D=∠BEF.
在△FDN与△BEF中,
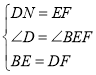 ,
,
∴△FDN≌△BEF,
∴FN=FB,
又∵NM=MB,
∴BM⊥MF


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】李明的作业本上有四道题:(1)a·a=a,(2)(2b)=8b,(3)-(x+1)=x+1,(4)4a÷(-2a)=-2a,如果你是他的数学老师,请找出他做错的题是( )
A.(1) B.(2) C.(3) D.(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪一个是假命题( )
A. 五边形外角和为360°
B. 切线垂直于经过切点的半径
C. (3,﹣2)关于y轴的对称点为(﹣3,2)
D. 抛物线y=x2﹣4x+2017对称轴为直线x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)

(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)当△CDE是直角三角形,且∠CDE=90° 时,求出点P的坐标;
(3)当△PBC的面积为![]() 时,求点E的坐标.
时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
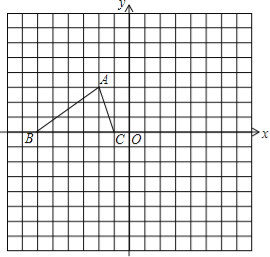
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八月份利川市政府计划在总费用2300元的限额内,租用汽车送234名运动员和6名教练到恩施州参加第二届全州青少年运动会,每辆汽车上至少要有1名教练.现有甲、乙两种大客车,它们的载客量和租金如下表:

(1)共需租多少辆汽车?
(2)有几种租车方案?
(3)最节省费用的是哪种租车方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com