
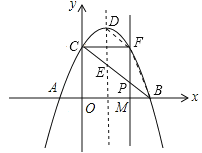
【题目】如图,抛物线![]() 与x轴相交的于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
与x轴相交的于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与C,B两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形.
②设△BCF的面积为S,求S与m的函数关系式;当m为何值时,S有最大值.

【答案】(1)A(﹣1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;(2)①m=2;②S=![]() (0<m<3),则当m=
(0<m<3),则当m=![]() 时,S取得最大值.
时,S取得最大值.
【解析】
试题分析:(1)对于抛物线![]() ,令x=0,得到y=3;
,令x=0,得到y=3;
令y=0,得到![]() ,即(x﹣3)(x+1)=0,解得:x=﹣1或x=3,则A(﹣1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
,即(x﹣3)(x+1)=0,解得:x=﹣1或x=3,则A(﹣1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
(2)①设直线BC的函数解析式为y=kx+b,把B(3,0),C(0,3)分别代入得:![]() ,解得:k=﹣1,b=3,∴直线BC的解析式为y=﹣x+3,当x=1时,y=﹣1+3=2,∴E(1,2),当x=m时,y=﹣m+3,∴P(m,﹣m+3),令
,解得:k=﹣1,b=3,∴直线BC的解析式为y=﹣x+3,当x=1时,y=﹣1+3=2,∴E(1,2),当x=m时,y=﹣m+3,∴P(m,﹣m+3),令![]() 中x=1,得到y=4,∴D(1,4),当x=m时,
中x=1,得到y=4,∴D(1,4),当x=m时,![]() ,∴F(m,
,∴F(m,![]() ),∴线段DE=4﹣2=2,∵0<m<3,∴yF>yP,∴线段PF=
),∴线段DE=4﹣2=2,∵0<m<3,∴yF>yP,∴线段PF=![]() ﹣(﹣m+3)=
﹣(﹣m+3)=![]() .连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,由
.连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,由![]() ,得到m=2或m=1(不合题意,舍去),则当m=2时,四边形PEDF为平行四边形;
,得到m=2或m=1(不合题意,舍去),则当m=2时,四边形PEDF为平行四边形;
②连接BF,设直线PF与x轴交于点M,由B(3,0),O(0,0),可得OB=OM+MB=3,∵S=S△BPF+S△CPF=![]() PFBM+
PFBM+![]() PFOM=
PFOM=![]() PF(BM+OM)=
PF(BM+OM)=![]() PFOB,∴S=
PFOB,∴S=![]() ×3(
×3(![]() ),即S=
),即S=![]() (0<m<3),则当m=
(0<m<3),则当m=![]() 时,S取得最大值.
时,S取得最大值.


科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某织布厂有 150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣 4 件,制衣一件需要布 1.5m,将布直接出售,每米布可获利 2 元,将布制成衣后出售,每件可获利 25 元,若每名工人只能做一项工作,且不计其他因素,设安排 x 名工人制衣.
(1)一天中制衣所获利润 元(用含 x 的式表示);
(2)一天中销售剩余的布所获利润为 元(用含 x 的式表示);
(3)一天当中安排 名工人制衣时,所获利润为 13712 元;
(4)一年按 300 天计算,一年中这个工厂所获利润最大值为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是反比例函数y= ![]() 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 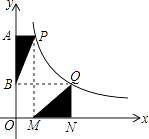
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是 . 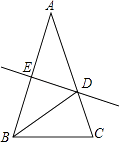
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com