
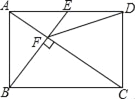
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() ;⑤S四边形CDEF=
;⑤S四边形CDEF=![]() S△ABF,其中正确的结论有( )
S△ABF,其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
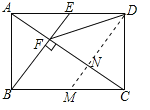
【解析】试题分析:过D作DM∥BE交AC于N,∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,AD=BC,∵BE⊥AC于点F,∴∠EAC=∠ACB,∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;
∵AD∥BC,∴△AEF∽△CBF,∴![]() ,∵AE=
,∵AE=![]() AD=
AD=![]() BC,∴
BC,∴![]() ,∴CF=2AF,故②正确,
,∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,∴四边形BMDE是平行四边形,∴BM=DE=![]() BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
∵tan∠CAD=![]() ,而CD与AD的大小不知道,∴tan∠CAD的值无法判断,故④错误;
,而CD与AD的大小不知道,∴tan∠CAD的值无法判断,故④错误;
∵△AEF∽△CBF,∴![]() ,∴S△AEF=
,∴S△AEF=![]() S△ABF,S△ABF=
S△ABF,S△ABF=![]() S矩形ABCD,∵S△ABE=
S矩形ABCD,∵S△ABE=![]() S矩形ABCD,S△ACD=
S矩形ABCD,S△ACD=![]() S矩形ABCD,∴S△AEF=
S矩形ABCD,∴S△AEF=![]() S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=
S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=![]() S矩形ABCD﹣
S矩形ABCD﹣![]() S矩形ABCD=
S矩形ABCD=![]() S矩形ABCD,∴S四边形CDEF=
S矩形ABCD,∴S四边形CDEF=![]() S△ABF,故⑤正确;
S△ABF,故⑤正确;
故选B.


科目:初中数学 来源: 题型:
【题目】刚刚升入初一,学习成绩优异但体育一般的王晴同学未雨绸缪,已经为将来的体育中考做起了准备.上周末她在家练习1分钟跳绳,以每分钟150下为基准,超过或不足的部分分别用正负数来表示,8次成绩(单位:下)分别是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成绩最好的一次比最差的一次多跳多少下?
(2)求王晴这8次跳绳的平均成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
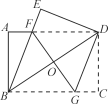
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1
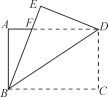
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题:“当a=2019,b=-3时,求多项式a2b3-![]() ab+b2-(4a2b3-
ab+b2-(4a2b3-![]() ab-b2)+(3a2b3+
ab-b2)+(3a2b3+![]() ab)-5的值”,马小虎做题时把a=2019题抄成a=-2019,但他做出的结果却是正确的,你知道这是怎么回事吗?请说明理由,并求出结果。
ab)-5的值”,马小虎做题时把a=2019题抄成a=-2019,但他做出的结果却是正确的,你知道这是怎么回事吗?请说明理由,并求出结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(教材回顾)
七上教材有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)
四边形有4个顶点,如果在它的内部再画n个点,并以这(n+4)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)
为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
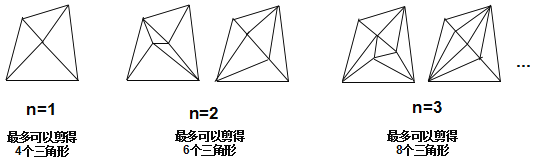
(问题解决)
(1)当四边形内有4个点时,最多剪得的三角形个数为______________;
(2)你发现的变化规律是:四边形内的点每增加1个,最多剪得的三角形增加______个;
(3)猜想:当四边形内点的个数为n时,最多可以剪得_______________个三角形;像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
请你尝试用归纳的方法探索4+6+8+10+…+2n+(2n+2)的和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份 | 2014 | 2015 | 2016 | 2017(预计) |
快递件总量(亿件) | 140 | 207 | 310 | 450 |
电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.
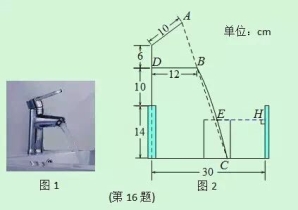
(第16题图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若tanA=![]() ,探究线段AB和BE之间的数量关系,并证明;
,探究线段AB和BE之间的数量关系,并证明;
(3)在(2)的条件下,若OF=1,求圆O的半径.
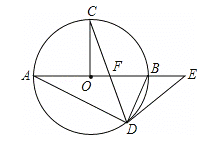
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com