练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有这样一道题：“当a＝2019，b＝－3时，求多项式a2b3－ab＋b2－(4a2b3－ab－b2)＋(3a2b3＋ab)－5的值”，马小虎做题时把a＝2019题抄成a＝－2019，但他做出的结果却是正确的，你知道这是怎么回事吗？请说明理由，并求出结果。

    【答案】见解析，13．

    【解析】

    原式去括号合并得到最简结果，即可作出判断．

    ∵a2b3-ab+b2-（4a2b3-ab-b2）+（3a2b3+ab）-5
    =a2b3-ab+b2-4a2b3+ab+b2+3a2b3+ab-5
    =2b2-5，
    ∴此整式化简后与a的值无关，
    ∴马小虎做题时把a=2019错抄成a=-2019，但他做出的结果却是正确的．
    当b=-3时，原式=2×（-3）2-5=13．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有这样一对数，如下表，第个数比第n个数大2(其中n是正整数)

    第1个

    第2个

    第3个

    第4个

    第5个

    ……

    a

    b

    c

    (1)第5个数表示为______；第7个数表示为_______.

    (2)若第10个数是5，第11个数是8，第12个数为9，则a＝______，b＝_____，c＝______.

    (3)第2019个数可表示为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？

    问题探究：不妨假设能搭成种不同的等腰三角形，为探究之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．

    探究一：

    （1）用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    此时，显然能搭成一种等腰三角形。所以，当时，

    （2）用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形

    所以，当时，

    （3）用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形

    若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形

    所以，当时，

    （4）用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形

    若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形

    所以，当时，

    综上所述，可得表①


    3

    4]

    5

    6


    1

    0

    1

    1

    探究二：

    （1）用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？

    （仿照上述探究方法，写出解答过程，并把结果填在表②中）

    （2）分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三

    角形？（只需把结果填在表②中）


    7

    8

    9

    10






    你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……

    解决问题：用根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？

    （设分别等于、、、，其中是整数，把结果填在表③中）











    问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角三角形ABC中，∠ABC=90°，∠C=30°，AB=4，以B为圆心，BA为半径作⊙B交BC于点D，旋转∠ABD交⊙B于点E、F，连接EF交AC、BC边于点G、H．

    （1）若BE⊥AC，求tan∠CGH的值；

    （2）若AG=4，求△BEF与△ABC重叠部分的面积；

    （3）△BHE是等腰三角形时，∠ABD逆时针旋转的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用小立方块搭一个几何体，使它从正面和上面看到的形状如图所示，从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数，请问：

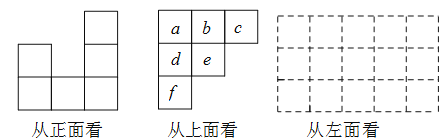
    （1），各表示几？ 答：_____ ，_____；

    （2）这个几何体最少由_____个小立方块搭成，最多由____个小立方块搭成；

    （3）能搭出满足条件的几何体共有____种情况，其中从左面看这个几何体的形状图共有____种，请在所给网格图中画出其中的任意一种．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三角形的第一边长为a2－2ab+b2，第二边比第一边的3倍少3，三角形的周长是5a2－7ab+5b2－1.

    （1）求这个三角形的第三边长；

    （2）当a=，b=－3时，求第三边长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD=；⑤S四边形CDEF=S△ABF，其中正确的结论有（　　）

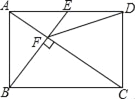
    A. 5个 B. 4个 C. 3个 D. 2个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：

    （1）求证：△BEF∽△DCB；

    （2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；

    （3）如图2过点Q作QG⊥AB，垂足为G，当t为何值时，四边形EPQG为矩形，请说明理由；

    （4）当t为何值时，△PQF为等腰三角形？试说明理由．

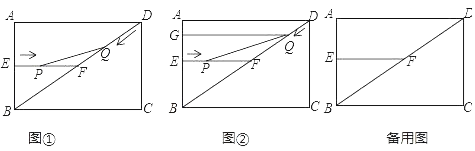
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值

    (1)，其中x=-2,y=1

    (2)﹣a2b+（3ab2﹣a2b）﹣2（2ab2﹣a2b），其中（a+1）2+|b+2|=0．

    查看答案和解析>>

    同步练习册答案