
【题目】邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】记y= f(![]() )=
)=![]() . 如: f(1)表示当x=1时y的值,即f(1)=
. 如: f(1)表示当x=1时y的值,即f(1)=![]() =
=![]() ;f(
;f(![]() )表示当
)表示当![]() =
=![]() 时y的值,即f(
时y的值,即f(![]() )=
)=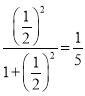 .
.
试回答:
(1)f(1)+f(2)+f(![]() )+f(3)+f(
)+f(3)+f(![]() )=__________ ;
)=__________ ;
(2)f(1)+f(2)+f(![]() )+f(3)+f(
)+f(3)+f(![]() )+……+f(
)+……+f(![]() )+f(
)+f(![]() )=__________.(结果用含
)=__________.(结果用含![]() 的代数式表示,
的代数式表示, ![]() 为正整数)
为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:任意两个数![]() ,按规则
,按规则![]() 扩充得到一个新数
扩充得到一个新数![]() ,称所得的新数
,称所得的新数![]() 为“如意数”.
为“如意数”.
(1)若![]() 直接写出
直接写出![]() 的“如意数”
的“如意数”![]() ;
;
(2)如果![]() ,求
,求![]() 的“如意数”
的“如意数”![]() ,并证明“如意数”
,并证明“如意数” ![]() ;
;
(3)已知![]() ,且
,且![]() 的“如意数”
的“如意数”![]() ,则
,则![]() _______________________(用含
_______________________(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )

A. a2﹣b2=(a﹣b)2 B. (a+b)2=a2+2ab+b2
C. (a﹣b)2=a2﹣2ab+b2 D. a2﹣b2=(a+b)(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )

A. AB=DB,∠ A=∠ D B. DB=AB,AC=DE C. AC=DE,∠C=∠E D. ∠ C=∠ E,∠ A=∠ D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是___个单位长度;△AOC与△BOD关于直线对称,则对称轴是___;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___度;
(2)连结AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解决有关问题:
我们知道:|x|=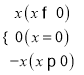 .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式=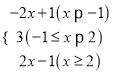 .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com