
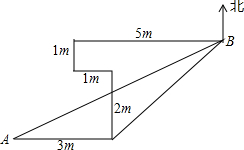
 如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.
如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 月份x | 1 | 2 |
| 再生资源处理量y(吨) | 40 | 50 |
| 1 |
| 2 |
| 157 |
| 156 |
| 158 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 有长为L的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.
有长为L的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
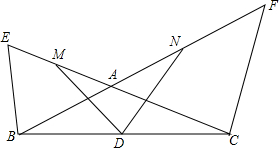 如图,BF、CE相交于点A,BE=BA,CA=CF,若D、M、N分别是BC,AE,AF的中点.
如图,BF、CE相交于点A,BE=BA,CA=CF,若D、M、N分别是BC,AE,AF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com