
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6,分别以AB、BC、CA为一边向形外作正方形,连接EF、GM、ND, 设△AEF,△CGM,△BND的面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() =___.
=___.

【答案】72
【解析】
作ER⊥FA交FA的延长线于R,作DH⊥NB交NB的延长线于H,作NT⊥DB交DB的延长线于T,,分别表示出三角形的面积,然后进行计算即可.
解:作ER⊥FA交FA的延长线于R,作DH⊥NB交NB的延长线于H,作NT⊥DB交DB的延长线于T,
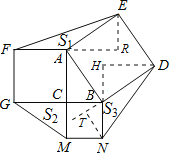
∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、正方形BCMN、正方形CAFG,
∵AE=AB,∠ARE=∠ACB,∠EAR=∠CAB,
∴△AER≌△ABC,
∴ER=BC=6,FA=AC=8,
∴S1=![]() ER·AF=
ER·AF=![]() ,S2=
,S2=![]() CG·CM=
CG·CM=![]() ,
,
同理可得HD=AR=AC,
∴S1=S2=S3=24.
所以![]()
故答案为:72.


科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“数学史”知识竞赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
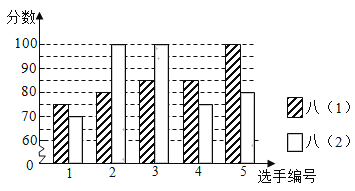
(1)根据图示填写下表a、b、c的值:
统计量 班别 | 平均数(分) | 中位数(分) | 众数(分) |
八年(1)班 | a | 85 | c |
八年(2)班 | 85 | b | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班的选于复赛成绩较好;
(3)通过计算八年(1)班5名选手的复赛成绩的方差S八(1)2=70,请你计算八年(2)班5名选手复赛成绩的方差并判断哪个班的选手复赛成绩较为均衡.
查看答案和解析>>
科目:初中数学 来源: 题型:
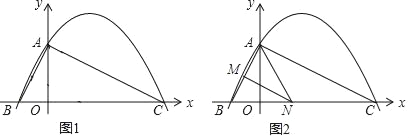
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
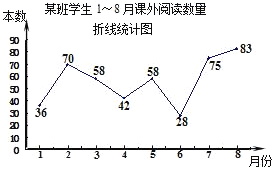
A.极差是47B.众数是42
C.中位数是58D.每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
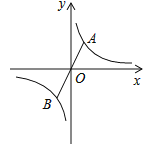
【题目】(2016湖北省荆门市)如图,已知点A(1,2)是反比例函数![]() 图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是______________.
图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
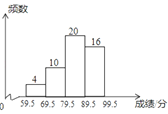
【题目】为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第三组(79.5~89.5)”的扇形的圆心角为多少度;
(2)若成绩在90分以上(含90分)的同学可以获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2-2x+3.
(1)将其配方成y=a(x-k)2+h的形式,并写出它的开口方向、对称轴及顶点坐标.
(2)在平面直角坐标系中画出函数的图象,并观察图象,当y≥0时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com