
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若BC=9,tan∠CDA=![]() ,求BE的长.
,求BE的长.

【答案】(1)证明见解析(2)![]()
【解析】分析: (1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=![]() =
=![]() ,易证Rt△CDO∽Rt△CBE,得到
,易证Rt△CDO∽Rt△CBE,得到![]() =
=![]() =
=![]() =
=![]() ,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
详解:
(1)证明:连OD,OE,如图,

∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,ED是切线,
∴ED=EB,∵OB=OD,
∴OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=![]() ,
,
∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴CD=![]() ×9=6,
×9=6,
在Rt△CBE中,设BE=x,
∴(x+6)2=x2+92,
解得x=![]() .
.
即BE的长为![]() .
.
点睛: 本题考查了切线的判定与性质:过半径的外端点与半径垂直的直线是圆的切线;也考查了圆周角定理的推论以及三角形相似的判定与性质,熟练应用切线判定是解题的关键.


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式![]() 的解集(满足不等式的所有解).
的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出![]() 恰好是3时
恰好是3时![]() 的值,并在数轴上表示为点
的值,并在数轴上表示为点![]() ,
,![]() ,如图所示.观察数轴发现,
,如图所示.观察数轴发现,
![]()
以点![]() ,
,![]() 为分界点把数轴分为三部分:
为分界点把数轴分为三部分:
点![]() 左边的点表示的数的绝对值大于3;
左边的点表示的数的绝对值大于3;
点![]() ,
,![]() 之间的点表示的数的绝对值小于3;
之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式![]() 的解集为:
的解集为:![]() 或
或![]() .
.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①![]() 的解集是 ;
的解集是 ;
②![]() 的解集是 .
的解集是 .
(2)求绝对值不等式![]() 的解集.
的解集.
(3)直接写出不等式![]() 的解集是 .
的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
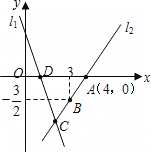
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一社团为了了解市区初中学生视力变化情况,从市区![]() 年入校的学生中随机抽取了部分学生连续三年的视力跟踪调查,并将收集到的数据进行整理,制成了折线统计图和扇形统计图.
年入校的学生中随机抽取了部分学生连续三年的视力跟踪调查,并将收集到的数据进行整理,制成了折线统计图和扇形统计图.
(1)这次接受调查的学生有_____________人;
(2)扇形统计图中“![]() ”所对应的圆心角有多少度?
”所对应的圆心角有多少度?
(3)现规定视力达到![]() 及以上为合格,若市区
及以上为合格,若市区![]() 年入校的学生共计
年入校的学生共计![]() 人,请你估计该届
人,请你估计该届![]() 名学生的视力在
名学生的视力在![]() 年有多少名学生合格.
年有多少名学生合格.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
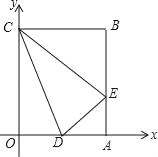
A. (1,3) B. (3,1) C. (4,1) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级各有150人参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下:
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:

分析数据:补全下列表格中的统计量:

得出结论:你认为抽取的学生哪个年级的成绩较为稳定?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com