
【题目】已知:如图,在△ABC中,AD是BC边上的高,∠C=30°,∠ABC=45°,BE是AC边上的中线.
(1)求证:AC=2BD;
(2)求∠CBE的度数;
(3)若点E到边BC的距离为![]() ,求BC的长.
,求BC的长.

【答案】(1)证明见解析;(2)∠CBE=15°;(3)BC=1+![]() .
.
【解析】
(1)根据直角三角形的性质得到AC=2AD,AD=BD,证明结论;
(2)连接DE,根据直角三角形的性质得到DE=EC=![]() AC,根据等腰三角形的性质计算即可;
AC,根据等腰三角形的性质计算即可;
(3)作EF⊥BC于F,根据直角三角形的性质求出EC,根据勾股定理计算,得到答案.
(1)证明:在Rt△ACD中,∠ADC=90°,∠C=30°,
∴AC=2AD,
在Rt△ABD中,∠ADB=90°,∠ABC=45°,
∴AD=BD,
∴AC=2BD;
(2)解:连接DE,
∵∠ADC=90°,BE是AC边上的中线,
∴DE=EC=![]() AC,
AC,
∴DE=DB,∠EDC=∠C=30°,
∴∠EBC=![]() ∠EDC=15°;
∠EDC=15°;
(3)作EF⊥BC于F,
则EC=2EF=1,
∴AC=2,BD=AD=1,
由勾股定理得,CD=![]() =
=![]() ,
,
∴BC=BD+CD=1+![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
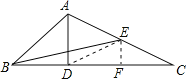
【题目】在等边△ABC中,D为射线BC上一点,CE是∠ACB外角的平分线,∠ADE=60°,EF⊥BC于F.
(1)如图1,若点D在线段BC上,证明:∠BAD=∠EDC;
(2)如图1,若点D在线段BC上,证明:①AD=DE;②BC=DC+2CF(提示:构造全等三角形);
(3)如图2,若点D在线段BC的延长线上,直接写出BC、DC、CF三条线段之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
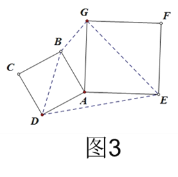
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明理由)
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明理由)
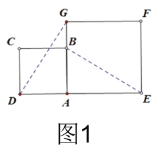
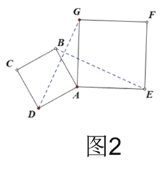
(1)如图2,小明将正方形ABCD绕点A逆时针旋转,旋转角为![]() (30﹤
(30﹤![]() ﹤180)
﹤180)
①连接DG,BE,求证:DG=BE且DG⊥BE;
②在旋转过程中,如图3,连接BG,GE,ED,DB,求出四边形BGED面积的最大值.
(2)如图4,分别取BG,GE,ED,DB的中点M,N,P,Q,连接MN,NP,PQ,QM,则四边形MNPQ的形状为 ,四边形MNPQ面积的最大值是 ,
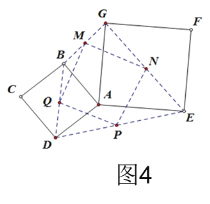
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)
(1)若点A的坐标为(a,0),则点C的坐标为 ;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队合作完成一项工程,需要12天完成,工程费用共36000元,若甲、乙两工程队单独完成此项工程,乙工程队所用的时间是甲工程队的1.5倍,乙工程队每天的费用比甲工程队少800元.
(1)问甲、乙两工程队单独完成此项工程各需多少天?
(2)若让一个工程队单独完成这项工程,哪个工程队的费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
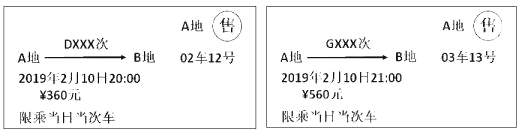
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com