
【题目】在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)
(1)若点A的坐标为(a,0),则点C的坐标为 ;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.

【答案】(1)(-a,0).(2)证明见解析;(3)∠ABE=2∠DEC.
【解析】
(1)利用对称性直接写成点C的坐标;
(2)根据三角形的内角和,等腰三角形的性质先判断出,∠ABE=∠BFE,进而得出BE=EF,在判断出,∠CBE=∠AEF,进而判定,△AEF≌△CBE,即可得出结论;
(3)设∠OBE=α,∠CBE=β,用三角形的内角和表示出∠ABE=2α+β,利用等腰三角形的性质表示出∠DEC=![]() (2α+β),即可得出结论.
(2α+β),即可得出结论.
(1)∵点A(a,0)与点C关于y轴对称,
∴C(-a,0),
故答案为(-a,0).
(2)设∠OBE=α,
∴∠BAO=2∠OBE=2α,∠BEF=∠BAO=α,
由对称得,OA=OC,
∵BO⊥AC,
∴AB=CB,
∴∠BAO=∠BCO=2α,
∴∠ABE=∠ABO+∠OBE=90°-α,
在△BEF中,∠BFE=180°-(∠BEF+∠EBF)=90°-α,
∴∠ABE=∠BFE,
∴BE=EF,
在Rt△AOB中,∠ABO=90°-2α,
∴∠ACB=2α,∠CBO=∠90°-2α,
∵∠OBE=α,
∴∠CBE=90°-3α,
在△BCE中,根据三角形的内角和得,∠BEC=90°+α,
∴∠AEF=180°-∠BEF-∠BEC=90°-3α,
∴∠CBE=∠AEF,
在△AEF和△CBE中,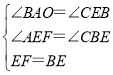 ,
,
∴△AEF≌△CBE,
∴AF=CE,
(3)设∠OBE=α,∠CBE=β,
∴∠CBO=α+β,由(1)知,∠ABO=∠CBO=α+β,
∴∠ABE=∠ABO+∠OBE=α+β+α=2α+β,
在Rt△OBE中,∠OEB=90°-α,
在△BDE中,BD=BE,
∴∠BED=90°-![]() β,
β,
∴∠DEC=180°-∠OEB-∠BED=![]() (2α+β),
(2α+β),
∵∠ABE=2α+β,
∴∠ABE=2∠DEC.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
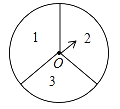
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1,2,3三个数字.小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束后得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏后得到的一组数恰好是方程x2﹣4x+3=0的解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)同题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.
∴∠APE=180°-∠PAB=180°-130°=50°.
∵AB∥CD.∴PE∥CD.
…………
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的思路,解答下面的问题:
如图3,AD∥BC,点P在射线OM上运动,∠MDP=∠α,∠BCP=∠β.
①当点P在A、B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.
②当点P在A、B两点外侧时(点P与点O不重合),请直接写出∠CPD,∠α,∠β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“a*b”:当a≥b时,a*b=a+2b;当a<b时,a*b=a-2b.
例如:3*(-4)=3+(-8)=-5,(-6)*12=-6-24=-30
(1)填空:(-4)*3= .
(2)若(3x-4)*(x+6)=(3x-4)+2(x+6),则x的取值范围为 ;
(3)已知(3x-7)*(3-2x)<-6,求x的取值范围;
(4)小明在计算(2x2-4x+8)*(x2+2x-2)时随意取了一个x的值进行计算,得出结果是-4,小丽告诉小明计算错了,问小丽是如何判断的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AD是BC边上的高,∠C=30°,∠ABC=45°,BE是AC边上的中线.
(1)求证:AC=2BD;
(2)求∠CBE的度数;
(3)若点E到边BC的距离为![]() ,求BC的长.
,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式,探究其中规律.
第1个等式:![]() ;
;
第2个等式:![]()
第3个等式:![]()
……
(1)第4个等式:![]() (直接填写结果);
(直接填写结果);
(2)根据以上规律请计算:![]() ;
;
(3)通过以上规律请猜想写出:![]() (直接填写结果).
(直接填写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
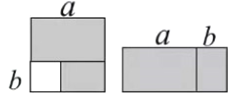
【题目】如图,从边长为![]() 的正方形内去掉一个边长为
的正方形内去掉一个边长为![]() 的小正方形,然后将剩余部分拼成一个长方形。
的小正方形,然后将剩余部分拼成一个长方形。
(1)上述操作所能验证的公式是 ;
(2)求大正方形和拼成的长方形的周长;
(3)用一根长为![]() 的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?
的铁丝围成一个长方形,什么情况下围成的面积最大,最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com