
【题目】如图,正方形![]() ,点
,点![]() 在
在![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() ,
,![]() 分别为点
分别为点![]() ,
,![]() 旋转后的对应点,连接
旋转后的对应点,连接![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
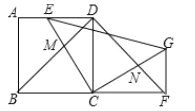
(1)求证![]() ;
;
(2)直接写出图中已经存在的所有等腰直角三角形.
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
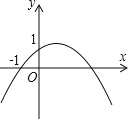
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
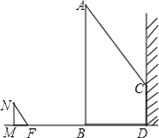
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
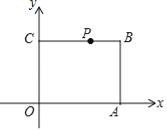
【题目】在平面直角坐标系中,点A的坐标为(5,0),点C的坐标为(0,4),四边形ABCO为矩形,点P为线段BC上的一动点,若△POA为等腰三角形,且点P在双曲线y=![]() 上,则k值可以是_____.
上,则k值可以是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
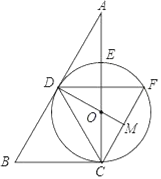
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦![]() 与AB平行,与DO的延长线交于M点.
与AB平行,与DO的延长线交于M点.
(1)求证:点M是CF的中点;
(2)若E是![]() 的中点,连结DF,DC,试判断△DCF的形状;
的中点,连结DF,DC,试判断△DCF的形状;
(3)在(2)的条件下,若BC=a,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“玉米楼”)坐落在风景如画的如意湖畔,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华决定用自己学到的知识测量“玉米楼”的高度.如图,刘明在点C处测得楼顶B的仰角为45°,王华在高台上的D处测得楼顶的仰角为40°.若高台DE的高为5米,点D到点C的水平距离EC为47.4米,A,C,E三点共线,求“玉米楼”AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题:
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
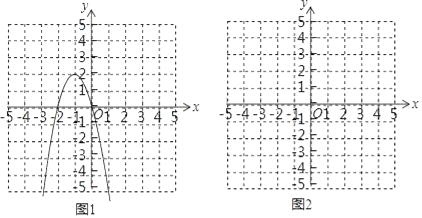
①构造函数,画出图象:
根据不等式特征构造二次函数y=﹣2x2﹣4x;抛物线的对称轴x=﹣1,开口向下,顶点(﹣1,2)与x轴的交点是(0,0),(﹣2,0),用三点法画出二次函数y=﹣2x2﹣4x的图象如图1所示;
②数形结合,求得界点:
当y=0时,求得方程﹣2x2﹣4x=0的解为 ;
③借助图象,写出解集:
由图象可得不等式﹣2x2﹣4x≥0的解集为 .
(2)利用(1)中求不等式解集的方法步骤,求不等式x2﹣2x+1<4的解集.
①构造函数,画出图象;
②数形结合,求得界点;
③借助图象,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式ax2+bx+c>0(a>0)的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com