

���� ��1����ͼ1������AAS֤����ABO�ա�BCD��
��2���������Ϊ8���AB�ij������ù��ɶ�����OB�ij������ɣ�1���е�ȫ�ȵó�CD��OD�ij���д����C�����꼴�ɣ�
��3���ɣ�1��ȫ�ȿɵõ�C������Ϊ��4��1����
��4����ͼ3������C��������EFGH�ĶԽ�����ʱ����C���H������С����OB=x������ȫ�������ζ�Ӧ����ȵ�PE=x-1������PH=3-x���ɡ�CPHΪ����ֱ�������Σ���ʽx=3-x�����x��ֵ����CH=$\sqrt{2}$PC���ó����ۣ�
��� 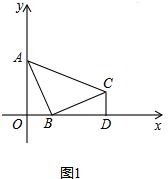 �⣺��1����ͼ1���ߡ�ABC�ǵ���ֱ�������Σ�
�⣺��1����ͼ1���ߡ�ABC�ǵ���ֱ�������Σ�
��AB=BC��
�ߡ�ABC=90�㣬
���ABO+��CBD=90�㣬
�ߡ�AOB=90�㣬
���BAO+��ABO=90�㣬
���CBD=��BAO��
�ߡ�AOB=��BDC=90�㣬
���ABO�ա�BCD��
��2����ͼ1���ߡ�ABC�����=8��
��$\frac{1}{2}$AB•BC=8��
��AB=BC��
��AB=BC=4��
��A��0��3����
��OA=3��
�ߡ�ABO�ա�BCD��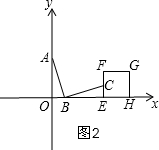
��BD=OA=3��
�ɹ��ɶ����ã�BO=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$��
��C��3+$\sqrt{7}$��$\sqrt{7}$����
��3����C���ڱ�EF��ʱ����ͼ2��
�ɣ�1���ã���AOB�ա�BEC��
��BE=OA=3��EC=OB��
��E��4��0����
��OE=4��
��OB=4-3=1��
��EC=OB=1��
��C��4��1����
��4����ͼ3������C��������EFGH�ĶԽ�����ʱ����C���H������С��
��C��CP��x����P��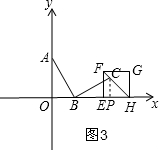
��OB=x��
�ߡ�AOB�ա�BPC��
��BP=AO=3��PC=OB=x��
��OE=4��
��EP=3+x-4=x-1��
��������EFGH�߳�Ϊ2��
��EH=2��
��PH=2-EP=2-��x-1��=3-x��
�ߡ�FHE=45�㣬
���CPHΪ����ֱ�������Σ�
��PC=PH��
��x=3-x��
x=$\frac{3}{2}$��
��CH=$\sqrt{2}$PC=$\frac{3}{2}\sqrt{2}$��
���� �������ı��ε��ۺ��⣬�����������Ρ�����ֱ�������Ρ�ȫ�������ε����ʣ�����ת�任���ϣ�ʹ�����ý�Ϊ���ӣ��������Ѷȣ���֪��תǰ����߶γ���ȣ������������˵���ֱ�������ε����ʵó�����ȼ��ǻ���Ĺ�ϵ���Դ���֤����������ȫ�ȣ��ó��������Ӷ�������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ�κ���y=kx+b��ͼ����������ֱ��ڵ�A��-2��0������B��0��2�������н����д�����ǣ�������
��ͼ��һ�κ���y=kx+b��ͼ����������ֱ��ڵ�A��-2��0������B��0��2�������н����д�����ǣ�������| A�� | y��x����������� | B�� | ��x=0ʱ��y=2 | ||
| C�� | k��0��b��0 | D�� | k��0��b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-1 | B�� | x=-2 | C�� | x=-2��x=1 | D�� | x=2��x=-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com