
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

【答案】(1)证明见解析.(2)![]() .
.
【解析】
试题分析:(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;
(2)在Rt△ADE中,由勾股定理得出方程,解方程求出BE,由勾股定理求出BD,得出OB,再由勾股定理求出EO,即可得出EF的长.
试题解析:(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
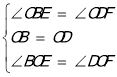 ,
,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE⊥EF,
设BE=x,则 DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=![]() ,
,
∵BD=![]() ,
,
∴OB=![]() BD=
BD=![]() ,
,
∵BD⊥EF,
∴EO=![]() ,
,
∴EF=2EO=![]() .
.


科目:初中数学 来源: 题型:
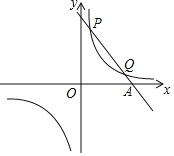
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
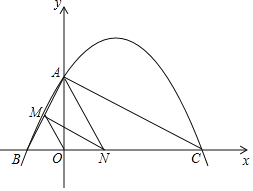
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽.甲、乙两个水槽中水的深度y(cm)与注水时间x(分)之间的关系如图2所示.根据图象解答下列问题: 
(1)图2中折线ABC表示槽中水的深度与注水时间之间的关系.线段DE表示槽中水的深度与注水时间之间的关系.点B的纵坐标的实际意义是 . 
(2)注水多长时间,甲、乙两个水槽中水的深度相同.
(3)若乙槽底面积为36cm2 , (壁厚不计),求乙槽中铁块的体积.
(4)若乙槽中铁块的体积为112cm3 , 则甲槽的底面积是cm2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①全等的两个图形一定成轴对称;②成轴对称的两个图形一定全等③轴对称图形的对称点一定在对称轴的两侧;④若点A、B关于直线MN对称,则直线MN垂直平分线段AB.正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A.互补的角不一定是邻补角B.互补的角若相等,则两个角都是直角
C.一个角的两个邻补角互为对顶角D.两个锐角的和是锐角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合采用全面调查(普查)方式的是( )
A.了解湖南卫视的收视率
B.了解湘江中草鱼种群数量
C.了解全国快递包裹产生包装垃圾的数量
D.了解某班同学“跳绳”的成绩
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com