
 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则| S△AEF |
| S△ABF |
| s |
| 4 |
| 1 |
| 2 |
| s |
| 2 |
| s |
| 2 |
| s |
| 4 |
| 1 |
| 2 |
| s |
| 2 |
| s |
| 2 |
| ||
|
| 1 |
| 4 |
| s |
| 6 |
| s |
| 6 |
| s |
| 4 |
| s |
| 4 |
| s |
| 6 |
| s |
| 12 |
| SAEF |
| S△ABF |
| ||
|
| 1 |
| 2 |
| 1 |
| 2 |


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
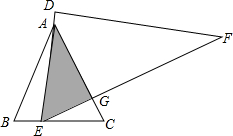 如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.
如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )
如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 一艘轮船沿长江顺流从武汉开往上海,行驶6小时后,发现船上一救生艇掉入江中,然后立即返回,再行驶3小时碰见救生艇.下图是轮船离出发地的距离与时间的函数关系,已知水流速度为5千米/时,则救生艇在轮船出发
一艘轮船沿长江顺流从武汉开往上海,行驶6小时后,发现船上一救生艇掉入江中,然后立即返回,再行驶3小时碰见救生艇.下图是轮船离出发地的距离与时间的函数关系,已知水流速度为5千米/时,则救生艇在轮船出发查看答案和解析>>
科目:初中数学 来源: 题型:
 如图为杨辉三角系数表,它有许多规律,如指导读者按规律写出如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的项.
如图为杨辉三角系数表,它有许多规律,如指导读者按规律写出如(a+b)n(其中n为正整数)展开式的系数,请你仔细观察下表中的规律,填出(a+b)4展开式中所缺的项.查看答案和解析>>
科目:初中数学 来源: 题型:
 据新华网2月28日公布,全国5个民族自治区参加第十二届全国人大代表会议的人数的平均数是49.8人,新疆地区60人,其余数据制成如图所示的不完整的条形统计图.
据新华网2月28日公布,全国5个民族自治区参加第十二届全国人大代表会议的人数的平均数是49.8人,新疆地区60人,其余数据制成如图所示的不完整的条形统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com