
【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示.
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是 元,小张应得的工资总额是 元,此时,小李种植水果 亩,小李应得的报酬是 元;
(2)当10<n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.

【答案】(1)140;2800;10;1500(2)z=120n+300(10<n≤30)(3)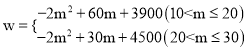
【解析】解:(1)140;2800;10;1500。
(2)当10<n≤30时,设z=kn+b(k≠0),
∵函数图象经过点(10,1500),(30,3900),
∴![]() ,解得
,解得![]() 。
。
∴当10<n≤30时, z与n之间的函数关系式为z=120n+300(10<n≤30)。
(3)当10<m≤30时,设y=k1m+b1,
∵函数图象经过点(10,160),(30,120),
∴![]() ,解得
,解得![]() 。
。
∴![]() 。
。
∵m+n=30,∴n=30-m。
∴①当10<m≤20时,10<n≤20,
![]() 。
。
②当20<m≤30时,0<n≤10,
![]() 。
。
∴w与m之间的函数关系式为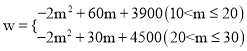 。
。
(1)根据图象数据解答即可:
由图可知,如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是(160+120)=140元,小张应得的工资总额是:140×20=2800元。此时,小李种植水果:30﹣20=10亩,小李应得的报酬是1500元。
(2)设z=kn+b(k≠0),然后利用待定系数法求一次函数解析式即可。
(3)先求出20<m≤30时y与m的函数关系式,再分①10<m≤20时,10<m≤20;②20<m≤30时,0<n≤10两种情况,根据总费用等于两人的费用之和列式整理即可得解。


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】某县九年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:
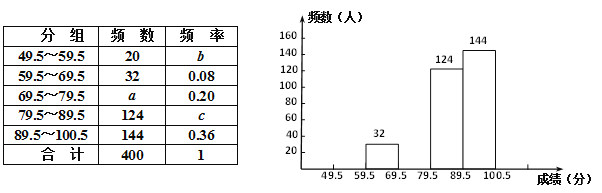
请结合图表完成下列问题:
(1)表中的![]() ,b= , c= ;
,b= , c= ;
(2)请把频数分布直方图补充完整;
(3)若将得分转化为等级,规定得分低于59.5分评为“D”,59.5~69.5分评为“C”,69.5~89.5分评为“B”,89.5~100.5分评为“A”,这次15000名学生中约有多少人被评为“B”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在AB边上,AD=CD,DE⊥AC于点E,CF∥AB,交DE的延长线于点F.
(1)如图1,求证:四边形ADCF是菱形; 
(2)如图2,当∠ACB=90°,∠B=30°时,在不添加辅助线的情况下,请直接写出图中与线段AC相等的线段(线段AC除外). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB

小易同学作法如下:
①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;
③以点O′为圆心,以OC长为半径作弧,交O′A于C
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′;
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.

老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片OABC放在平面直角坐标系中,0为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠,使点A落在点Q处.
(1)如图①,当点Q恰好落在OB上时.求点p的坐标;
(2)如图②,当点P是AB中点时,直线OQ交BC于M点.
①求证:MB=MQ;②求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x﹣0|,也就是说|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为:|x﹣y|表示在数轴上数x、y对应点之间的距离;在解题中,我们常常运用绝对值的几何意义.
①解方程|x|=2,容易看出,在数轴上与原点距离为2的点对应的数为±2,即该方程的解为x=±2.
②在方程|x﹣1|=2中,x的值就是数轴上到1的距离为2的点对应的数,显然x=3或x=﹣1.
③在方程|x﹣1|+|x+2|=5中,显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值,在数轴上1和﹣2的距离为3,满足方程的x的对应点在1的右边或﹣2的左边.若x的对应点在1的右边,由图示可知,x=2;同理,若x的对应点在﹣2的左边,可得x=﹣3,所以原方程的解是x=2或x=﹣3.根据上面的阅读材料,解答下列问题:
(1)方程|x|=5的解是_______________.
(2)方程|x﹣2|=3的解是_________________.
(3)画出图示,解方程|x﹣3|+|x+2|=9.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com