
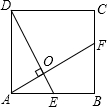
 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则| AO |
| DO |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
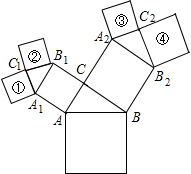 如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.
如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.查看答案和解析>>
科目:初中数学 来源: 题型:
| 平均数 | 众数 | 方差 | |||
| 甲 | 10 | ||||
| 乙 | 10 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
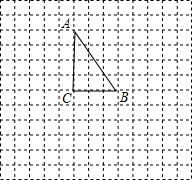 如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.
如图,△ABC的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:
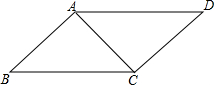 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,
如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com