
【题目】如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
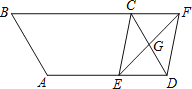
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.
【答案】(1)见解析;(2)①7;②4.
【解析】
(1)根据平行四边形的性质得出CF平行ED,再根据三角形的判定方法判定△CFG≌△EDG,从而得出FG=CG,根据平行四边形的判定定理,即可判断四边形CEDF为平行四边形.
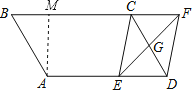
(2)①过A作AM⊥BC于M,根据直角三角形边角关系和平行四边形的性质得出DE=BM,根据三角形全等的判定方法判断△MBA≌△EDC,从而得出∠CED=∠AMB=90°,根据矩形的判定方法,即可证明四边形CEDF是矩形.
②根据题意和等边三角形的性质可以判断出CE=DE,再根据菱形的判定方法,即可判断出四边形CEDF是菱形.
(1)证明:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,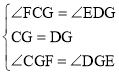
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=7时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=6,
∴BM=3,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,
∵AE=7,
∴DE=3=BM,
在△MBA和△EDC中,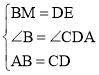 ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:7;
②当AE=4时,四边形CEDF是菱形,
理由是:∵AD=10,AE=4,
∴DE=6,
∵CD=6,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.


科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元.则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
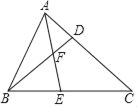
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若买3根跳绳和6个毽子共72元;买1根跳绳和5个毽子共36元.
(1)跳绳、毽子的单价各是多少元?
(2)元旦促销期间,所有商品按同样的折数打折销售,买10根跳绳和10个毽子只需180元,问商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
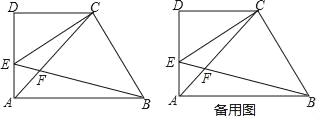
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是直线y=x+4与坐标轴的交点,直线y=-2x+b过点B,与x轴交于点C.
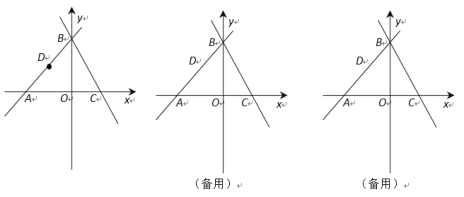
(1)求A,B,C三点的坐标;
(2)点D是折线A—B—C上一动点.
①当点D是AB的中点时,在x轴上找一点E,使ED+EB的和最小,用直尺和圆规画出点E的位置(保留作图痕迹,不要求写作法和证明),并求E点的坐标.
②是否存在点D,使△ACD为直角三角形,若存在,直接写出D点的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
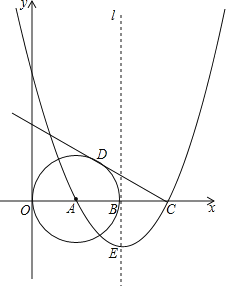
【题目】如图,已知点A(2,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A,抛物线与x轴的另一个交点为点C,抛物线的顶点为点E,如果CO=2BE,求此抛物线的解析式;
(2)过点C作⊙A的切线CD,D为切点,求此切线长;
(3)点F是切线CD上的一个动点,当△BFC与△CAD相似时,求出BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com