
【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元.则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
【答案】(1)y=﹣10x2+100x+2000;(2)售价定为65元时,商场所获的利润最大,最大利润是2250元;
(3)当62≤售价≤68时,每个月的利润不低于2160元.
【解析】
试题分析:(1)根据题意,得出每件商品的利润以及商品总的销量,即可得出y与x的函数关系式;
(2)根据题意利用配方法得出二次函数的顶点形式,进而得出当y的最大值;
(3)利用(1)中的函数解析式建立不等式,画出图象,利用图象求得不等式的解集即可.
试题解析:(1)每件商品的利润为:(60﹣50+x)元,
总销量为:(200﹣10x)件,
商品利润为:
y=(60﹣50+x)(200﹣10x)
=(10+x)(200﹣10x)
=﹣10x2+100x+2000;
(2)y=﹣10x2+100x+2000
=﹣10(x2﹣10x)+2000
=﹣10(x﹣5)2+2250;
故当x=5时,最大月利润y=2250元,
这时售价为60+5=65(元),
答:售价定为65元时,商场所获的利润最大,最大利润是2250元;
(3)由(1)知,y=﹣10x2+100x+2000(0<x≤12).
﹣10x2+100x+2000≥2160,
令﹣10x2+100x+2000=0
解得,x=2或x=8,60+2=62,60+8=68,
如图,
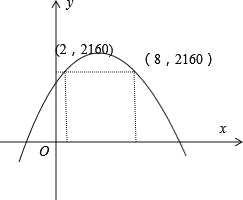
所以当62≤售价≤68时,每个月的利润不低于2160元.


科目:初中数学 来源: 题型:
【题目】下列各对等式,是根据等式的性质进行变形的,其中错误的是( ).
A.4x-1=5x+2→x=-3
B.![]() -
- ![]() =23→
=23→ ![]() -
- ![]() =230
=230
C.![]() +
+ ![]() =0.23→
=0.23→ ![]() +
+ ![]() =23
=23
D.![]() -
- ![]() =1→2(x+5)-3(x-3)=6
=1→2(x+5)-3(x-3)=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题及函数y=x,y=x2和y=![]() 的图象:
的图象:
①如果![]() >a>a2,那么0<a<1;
>a>a2,那么0<a<1;
②如果a2>a>![]() ,那么a>1;
,那么a>1;
③如果![]() >a2>a,那么﹣1<a<0;
>a2>a,那么﹣1<a<0;
④如果a2>![]() >a,那么a<﹣1.
>a,那么a<﹣1.
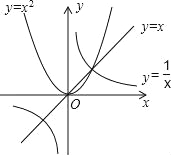
A.正确的命题是①② B.错误的命题是②③④
C.正确的命题是①④ D.错误的命题只有③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=90°,AC=BD,AC⊥BD,若AB=4, AD=5,则DC的长 ( ).

A. 7 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是中线,∠ACB=90°,AC=BC,点E,F分别为AB,AC上的动点(均不与端点重合),且CE⊥BF,垂足为H,BF与CD相交于G.
(1)求证:AE=CG;
(2)当线段AE,CF之间满足什么数量关系时,BF为△ABC的角平分线?请说明理由.
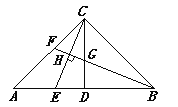
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.A、B、C三点在数轴上,A表示的数为-10,B表示的数为14,点C在点A与点B之间,且AC=BC.![]()
(1)求A、B两点间的距离;![]()
(2)求C点对应的数;
(3)甲、乙分别从A、B两点同时相向运动,甲的速度是1个单位长度/s,乙的速度是2个单位长度/s,求相遇点D对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
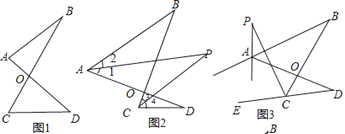
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
【拓展延伸】
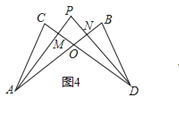
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com