
【题目】如图,在△ABC中,CD是中线,∠ACB=90°,AC=BC,点E,F分别为AB,AC上的动点(均不与端点重合),且CE⊥BF,垂足为H,BF与CD相交于G.
(1)求证:AE=CG;
(2)当线段AE,CF之间满足什么数量关系时,BF为△ABC的角平分线?请说明理由.
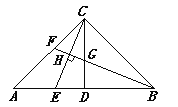
【答案】(1)证明见解析;(2)当AE=CF时,BF为△ABC的角平分线.理由见解析.
【解析】试题分析:
(1)由等腰直角三角形的性质可证得∠A=∠BCG=45°,再由∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,得到∠ACE=∠CBG,这样结合AC=BC,由“ASA”可证△ACE≌△CBG就可得到结论了;
(2)当AE=CF时,BF是△ABC的角平分线;由AE=CF,AE=CG,可得CF=CG,这样∠CFG=∠CGF,进一步就可证得∠CBF=∠DBF,从而可得BF平分∠ABC.
试题解析:
(1)∵∠ACB=90°,AC=BC,CD是中线,
∴∠ACE+∠BCE=90°,∠A=∠ABC=∠BCG=45°.
∵CE⊥BF,垂足为H,∴∠BHC=90°.
∴∠CBG+∠BCE=90°.
∴∠ACE=∠CBG.
在△ACE和△CBG中: 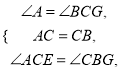
∴△ACE≌△CBG.
∴AE=CG.
(2)当AE=CF时,BF为△ABC的角平分线.
理由如下:∵AE=CF,AE=CG.
∴CF=CG.
∴∠CFG=∠CGF.
∵∠CFG=∠A+∠ABF,∠CGF=∠BCG+∠CBF,∠A=∠BCG,
∴∠ABF=∠CBF.即BF为△ABC的角平分线.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】![]()
=1﹣ ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]()
将以上三个等式两边分别相加得: ![]() +
+ ![]() +
+ ![]() =1﹣
=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() =
= ![]()
(1)猜想并写出: ![]() .
.
(2)直接写出下列各式的计算结果:
① ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() = .
= .
② ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() = .
= .
(3)探究并计算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①有一列数:1,-2,-3,4,-5,-6,7,-8,…那么接下来的3个数分别是 , , ;
②有一列数: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,….那么接下来的第7个数是 .
,….那么接下来的第7个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
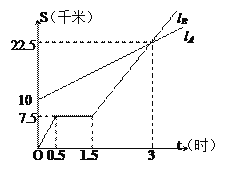
【题目】如图, ![]() 与
与 ![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车同一路上行驶的路程
骑车同一路上行驶的路程![]() 与时间
与时间![]() 的关系.
的关系.
(1)![]() 出发时与
出发时与![]() 相距多少千米?
相距多少千米?
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时?
(3)![]() 出发后经过多少小时与
出发后经过多少小时与![]() 相遇?
相遇?
若![]() 的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与
的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与![]() 相遇?在图中表示出这个相遇点
相遇?在图中表示出这个相遇点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元.则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),如图中的折线表示
(千米),如图中的折线表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
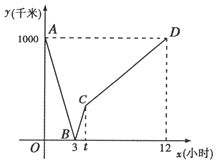
根据图象进行以下探究:
(1)西宁到西安两地相距_________千米,两车出发后___________小时相遇;
普通列车到达终点共需__________小时,普通列车的速度是___________千米/小时.
(2)求动车的速度;
(3)普通列车行驶![]() 小时后,动车的达终点西宁,求此时普通列车还需行驶多少千米到达西安?
小时后,动车的达终点西宁,求此时普通列车还需行驶多少千米到达西安?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续走了1.5千米到达小红家,又向西走了10千米到达小刚家,最后回到百货大楼. ![]()
(1)以百货大楼为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.05升,那么这辆货车共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com