
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续走了1.5千米到达小红家,又向西走了10千米到达小刚家,最后回到百货大楼. ![]()
(1)以百货大楼为原点,以向东的方向为正方向,用1个单位长度表示1千米,请你在数轴上表示出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.05升,那么这辆货车共耗油多少升?
【答案】
(1)解:如图所示:A、B、C分别表示小明、小红、小刚家
![]()
(2)解:小明家与小刚家相距:4﹣(﹣4.5)=8.5(千米)
(3)解:这辆货车此次送货共耗油:(4+1.5+10+4.5)×0.05=1(升).
答:小明家与小刚家相距8.5千米,这辆货车此次送货共耗油1升
【解析】(1)根据已知,以百货大楼为原点,以向东为正方向,用1个单位长度表示1千米一辆货车从百货大楼出发,向东走了4千米,到达小明家,继续向东走了1.5千米到达小红家,然后西走了8.5千米,到达小刚家,最后返回百货大楼,则小明家、小红家和小刚家在数轴上的位置可知.(2)用小明家的坐标减去与小刚家的坐标即可.(3)这辆货车一共行走的路程,实际上就是4+1.5+10+4.5=20(千米),货车从出发到结束行程共耗油量=货车行驶每千米耗油量×货车行驶所走的总路程.
【考点精析】通过灵活运用正数与负数和数轴,掌握大于0的数叫正数;小于0的数叫负数;0既不是正数也不是负数;正数负数表示具有相反意义的量;数轴是规定了原点、正方向、单位长度的一条直线即可以解答此题.


科目:初中数学 来源: 题型:
【题目】解方程2y-3=2-3y时,移项正确的是( )
A. 2y=2-3y-3 B. 2y-3-3y=2
C. 2y+3y=2+3 D. 2y-3y=2-3
查看答案和解析>>
科目:初中数学 来源: 题型:
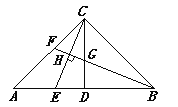
【题目】如图,在△ABC中,CD是中线,∠ACB=90°,AC=BC,点E,F分别为AB,AC上的动点(均不与端点重合),且CE⊥BF,垂足为H,BF与CD相交于G.
(1)求证:AE=CG;
(2)当线段AE,CF之间满足什么数量关系时,BF为△ABC的角平分线?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则tan∠AHE的值为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=-2x+12与x轴交于点A,与y轴交于点B,
与直线y=x交于点C.
(1)求点C的坐标
(2)求三角形OAC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
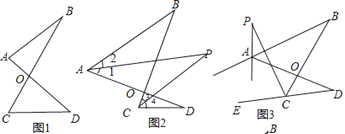
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
【拓展延伸】
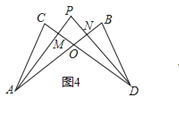
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进营业额不断增长,某大型超市决定购进甲、乙两种商品,已知甲种商品每件进价为150元,售价为168元;乙种商品每件进价为120元,售价为140元,该超市用42000元购进甲、乙两种商品,销售完后共获利5600元.
(1)该超市购进甲、乙两种商品各多少件?
(2)超市第二次以原价购进甲、乙两种商品共400件,且购进甲种商品的件数多于乙种商品的件数,要使第二次经营活动的获利不少于7580元,共有几种进货方案?写出利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com