
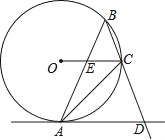
【题目】如图⊙O是△ABC的外接圆,∠ABC=45°,延长BC于D,连接AD,使得AD∥OC,AB交OC于E.
(1)求证:AD与⊙O相切;
(2)若AE=2![]() ,CE=2.求⊙O的半径和AB的长度.
,CE=2.求⊙O的半径和AB的长度.
【答案】(1)见解析;(2)AB=![]() .
.
【解析】
(1)连接OA,要证明切线,只需证明OA⊥AD,根据AD∥OC,只需得到OA⊥OC,根据圆周角定理即可证明;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=
,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=![]() ,然后根据勾股定理计算出AH=
,然后根据勾股定理计算出AH=![]() ,再利用垂径定理得出AB=2AH═
,再利用垂径定理得出AB=2AH═![]() .
.
(1)连接OA,
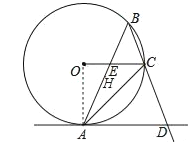
∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴OA⊥OC;
又∵AD∥OC,
∴OA⊥AD,
∴AD是⊙O的切线.
(2)设⊙O的半径为R,则OA=R,OE=R﹣2,AE=2![]() ,
,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R﹣2)2=(2![]() )2,解得R=4,
)2,解得R=4,
作OH⊥AB于H,如图,
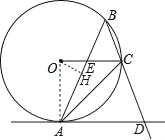
OE=OC﹣CE=4﹣2=2,
则AH=BH,
∵![]() OHAE=
OHAE=![]() OEOA,
OEOA,
∴OH=![]() =
=![]() =
=![]() ,
,
在Rt△AOH中,AH=![]() =
=![]() ,
,
∵OH⊥AB,
∴AB=2AH=![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 经过点
经过点![]() ,则
,则![]() ________;若点
________;若点![]() 为该曲线上的一点,过点
为该曲线上的一点,过点![]() 作
作![]() 轴、
轴、![]() 轴的垂线,分别交直线
轴的垂线,分别交直线![]() 于点
于点![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,则
,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
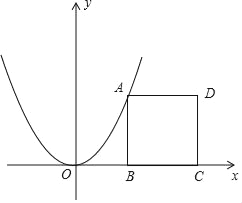
【题目】如图,正方形ABC的顶点A在抛物线y=x2上,顶点B,C在x轴的正半轴上,且点B的坐标为(1,0)
(1)求点D坐标;
(2)将抛物线y=x2适当平移,使得平移后的抛物线同时经过点B与点D,求平移后抛物线解析式,并说明你是如何平移的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市2013年体育中考考试方案公布后,同学们将根据自己平的运动成绩确定自己的报考项目,下面是小亮同学近期在两个项目中连续五次测试的(得分情况得分统计表得分折线图)
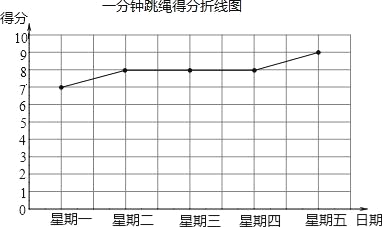
立定跳远测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
(1)请根据图表信息,分别计算小亮这两个项目测试成绩的平均数和方差;
(2)根据以上信息,你认为在立定跳远和一分钟跳绳这两个项目中,小亮应选择哪个项目作为体育考试的报考项目?并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车,乙步行均从![]() 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向![]() 地行驶,其中甲先出发到达
地行驶,其中甲先出发到达![]() 地,停留
地,停留![]() 分钟后,按原路原速返回到
分钟后,按原路原速返回到![]() 地,乙则一直步行到
地,乙则一直步行到![]() 地,如图是甲乙两人之间的距离
地,如图是甲乙两人之间的距离![]() 米与甲用时
米与甲用时![]() 之间的部分函数图象.
之间的部分函数图象.
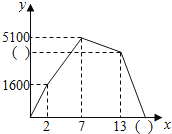
(1)请直接写出甲,乙两人的速度,并将图中的( )内填上正确的值;
(2)求甲从![]() 地返回到与乙相遇这段过程中,
地返回到与乙相遇这段过程中,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求乙在向![]() 地行驶过程中甲乙两人相距
地行驶过程中甲乙两人相距![]() 米时,甲所用时间及
米时,甲所用时间及![]() ,
,![]() 两地的距离.
两地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是______ cm.
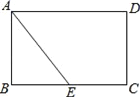
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com