
����Ŀ���������г����Ҳ��о���![]() �س������Ը��Ե��ٶ�������
�س������Ը��Ե��ٶ�������![]() ����ʻ�����м��ȳ�������
����ʻ�����м��ȳ�������![]() �أ�ͣ��
�أ�ͣ��![]() ���Ӻ�ԭ·ԭ�ٷ��ص�
���Ӻ�ԭ·ԭ�ٷ��ص�![]() �أ�����һֱ���е�
�أ�����һֱ���е�![]() �أ���ͼ�Ǽ�������֮��ľ���
�أ���ͼ�Ǽ�������֮��ľ���![]() �������ʱ
�������ʱ![]() ֮��IJ��ֺ���ͼ��
֮��IJ��ֺ���ͼ��
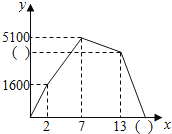
��1����ֱ��д���ף������˵��ٶȣ�����ͼ�еģ���������������ȷ��ֵ��
��2����״�![]() �ط��ص�����������ι����У�
�ط��ص�����������ι����У�![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3����������![]() ����ʻ�����м����������
����ʻ�����м����������![]() ��ʱ��������ʱ�估
��ʱ��������ʱ�估![]() ��
��![]() ���صľ��룮
���صľ��룮
���𰸡���1��4500�ף�18���ӣ���2��y=-900x+16200����3��������B����ʻ�����м����������2700��ʱ��������ʱ��Ϊ![]() �ֻ�15�֣�A��B���صľ���Ϊ5600�ף�
�ֻ�15�֣�A��B���صľ���Ϊ5600�ף�
��������
��1�����жϳ��ĸ�ʱ����ڼ��Ҷ��˵��˶������Ȼ��������ٶȣ��ٸ����������з�������ҵ��ٶȼ��ɣ����ݼ���Ϣ6������ʽ��⼴�ɵõ�13���ӵ�y��ֵ���ٸ��������������13���Ӻ�������ʱ�䣬Ȼ����⼴�ɣ�
��2�����ô���ϵ������һ�κ�������ʽ��ɣ�
��3����׳���x���Ӻ��������2700�ף�Ȼ���2��7����ʱ�������������г�������⼴�ɣ�13����֮���ü���B����B�صľ����ȥ�Ҳ��еľ����г�������⼴�ɣ��ٸ��ݼ����ҵص�ʱ��Ϊ7������ʽ��⼴�ɵõ����ؼ�ľ��룮
��1��������ã�0��t��2ʱ�����ȳ�����
2��t��7�����Ҷ��˹�ͬ��ʻ��
7��t��13����ͣ��B�أ�
13����֮�״�B����A����ʻ���Ҵ�A����B����ʻ��
���ԣ����ٶ�=![]() =800��/�֣�
=800��/�֣�
���ҵ��ٶ�Ϊv��/�֣�
��800����7-2��-��7-2��v=5100-1600��
���v=100��
5100-100��6=5100-600=4500�ף�
4500����800+100��=5��
13+5=18�֣�
���ԣ�ͼ��������������������ݷֱ���4500�ף�18���ӣ�
��2����һ�κ�������ʽΪy=kx+b������1���õ��ĵ����ɵã�
��![]() ��
��
���![]() ��
��
���ԣ�y=-900x+16200��
��3����׳���x���Ӻ��������2700�ף�
��2��7����ʱ��800��x-2��-100��x-2��=2700-1600��
���x=![]() ��
��
13����֮��-900x+16200=2700��
���x=15��
��7����ʱ���״�A�ص���B�أ�
��A��B���ؼ�ľ���Ϊ7��800=5600�ף�
��������B����ʻ�����м����������2700��ʱ��������ʱ��Ϊ![]() �ֻ�15�֣�A��B���صľ���Ϊ5600�ף�
�ֻ�15�֣�A��B���صľ���Ϊ5600�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У���E��F�ֱ���AB��AD�ϣ���EFB=2��AFE=2��BCE��CD=9��CE=20�����߶�AF�ij�Ϊ�� ����
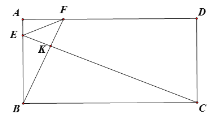
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() �ǵ���ֱ�������Σ�����
�ǵ���ֱ�������Σ�����![]() ��б��
��б��![]() ���ڵ�ֱ���ϣ���
���ڵ�ֱ���ϣ���![]() Ϊֱ�DZ�������ֱ��������
Ϊֱ�DZ�������ֱ��������![]() ������
������![]() ��̽��������������⣺
��̽��������������⣺
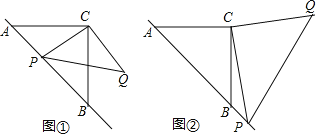
��1����ͼ�٣�����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬
���߶�![]() �� ����
�� ����
�ڲ��룺����![]() ����
����![]() ��
��![]() ��λ�ù�ϵΪ�� ����
��λ�ù�ϵΪ�� ����![]() ��
��![]() ��
��![]() ����֮���������ϵΪ�� ����
����֮���������ϵΪ�� ����
��2����ͼ�ڣ�����![]() ��
��![]() ���ӳ����ϣ��ڣ�1����������Ľ����Ƿ���Ȼ��������������ͼ�ڸ���֤�����̣�
���ӳ����ϣ��ڣ�1����������Ľ����Ƿ���Ȼ��������������ͼ�ڸ���֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
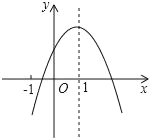
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��������6�����ۣ�
��abc��0��
��b��a��c��
��4a+2b+c��0��
��2c��3b��
��a+b��m��am+b������m��1��ʵ����
��2a+b+c��0��������ȷ�Ľ��۵���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
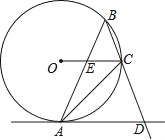
����Ŀ����ͼ��O�ǡ�ABC�����Բ����ABC��45�㣬�ӳ�BC��D������AD��ʹ��AD��OC��AB��OC��E��
��1����֤��AD����O���У�
��2����AE��2![]() ��CE��2������O�İ뾶��AB�ij��ȣ�
��CE��2������O�İ뾶��AB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DB��AC����DB=![]() AC��E��AC���е㣮
AC��E��AC���е㣮
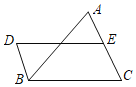
��1����֤���ı���BDEC��ƽ���ı��Σ�
��2������AD��BE����ABC����һ�������� ��ʹ�ı���DBEA�Ǿ��Σ�����˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����2��2����B����3����2��
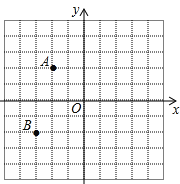
��1������D���A����y���Գƣ����D������Ϊ ��
��2������B������ƽ��5����λ������ƽ��1����λ�õ���C�����C������Ϊ ��
��3����A��B��C��D��ɵ��ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
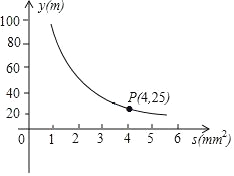
����Ŀ����Թ�������ʵ������������Ĺ����о�������ѧ֪ʶ��һ������������������棬�������ܳ���y��m���������Ĵ�ϸ����������S��mm2���ķ�������������ͼ����ͼ��ʾ��
��1��д��y��m����S��mm2���ĺ�����ϵʽ��
��2����������2mm2ʱ���������ܳ����Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ı�
�ı�![]() ��
��![]() Ϊ�߷ֱ�������
Ϊ�߷ֱ�������![]() ��
��![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ��
��
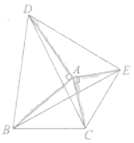
��1����֤��![]() ��
��
��2�����ж�![]() ��
��![]() �����֮���������ϵ����˵�����ɣ�
�����֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com