
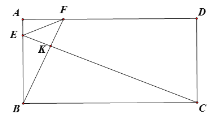
【题目】在矩形ABCD中,点E、F分别在AB、AD上,∠EFB=2∠AFE=2∠BCE,CD=9,CE=20,则线段AF的长为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
如图,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠ECB=2a,则∠AFB=3a,进而求出BH=CH=EH=10,∠HBC=∠HCB=a,再根据AD∥BC求出EF∥BH,进而得出△EFG和△BGH均为等腰三角形,则BF=EH=10,再根据勾股定理即可求解.
如图,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠ECB=2a,则∠AFB=3a,

∵在矩形ABCD中有AD∥BC,∠A=∠ABC=90°,
∴△BCE为直角三角形,
∵点H为斜边CE的中点,CE=20,
∴BH=CH=EH=10,∠HBC=∠HCB=a,
∵AD∥BC,
∴∠AFB=∠FBC=3a,
∴∠GBH=3a-a=2a=∠EFB,
∴EF∥BH,
∴∠FEG=∠GHB=∠HBC+∠HCB=2a=∠EFB=∠GBH,
∴△EFG和△BGH均为等腰三角形,
∴BF=EH=10,
∵AB=CD=9,
∴![]() .
.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木箱中装有卡片共50张,这些卡片共有三种,它们分别标有1、2、3的字样,除此之外其他都相同,其中标有数字2卡片的张数是标有数字3卡片的张数的3倍少8张.已知从箱子中随机摸出一张标有数字1卡片的概率是![]() .
.
(1)求木箱中装有标1的卡片张数;
(2)求从箱子中随机摸出一张标有数字3的卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 经过点
经过点![]() ,则
,则![]() ________;若点
________;若点![]() 为该曲线上的一点,过点
为该曲线上的一点,过点![]() 作
作![]() 轴、
轴、![]() 轴的垂线,分别交直线
轴的垂线,分别交直线![]() 于点
于点![]() 、
、![]() 两点,若直线
两点,若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,则
,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
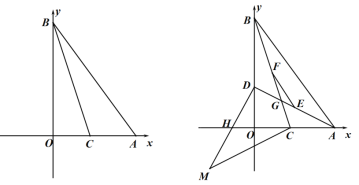
【题目】如图,在平面直角坐标系中,O为坐标原点,A点的坐标为(18,0),B点的坐标为(0,24).
(1)求AB的值;
(2)点C在OA上,且BC平分∠OBA,求点C的坐标;
(3)在(2)的条件下,点M在第三象限,点D为y轴上的一个点,连接DM交x轴于点H,连接CM,点F为BC的中点,点E为AD的中点,AD与BC交于点G,,点H为DM的中点,当∠MCG-∠DGF=∠OAB,且AD=CM时,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因为![]() ,令
,令![]() =0,则(x+3)(x-2)=0,x=-3或x=2,反过来,x=2能使多项式
=0,则(x+3)(x-2)=0,x=-3或x=2,反过来,x=2能使多项式![]() 的值为0.
的值为0.
利用上述阅读材料求解:
(1)若x﹣4是多项式x2+mx+8的一个因式,求m的值;
(2)若(x﹣1)和(x+2)是多项式![]() 的两个因式,试求a,b的值;
的两个因式,试求a,b的值;
(3)在(2)的条件下,把多项式![]() 因式分解的结果为 .
因式分解的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车,乙步行均从![]() 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向![]() 地行驶,其中甲先出发到达
地行驶,其中甲先出发到达![]() 地,停留
地,停留![]() 分钟后,按原路原速返回到
分钟后,按原路原速返回到![]() 地,乙则一直步行到
地,乙则一直步行到![]() 地,如图是甲乙两人之间的距离
地,如图是甲乙两人之间的距离![]() 米与甲用时
米与甲用时![]() 之间的部分函数图象.
之间的部分函数图象.
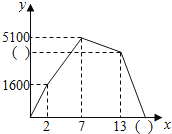
(1)请直接写出甲,乙两人的速度,并将图中的( )内填上正确的值;
(2)求甲从![]() 地返回到与乙相遇这段过程中,
地返回到与乙相遇这段过程中,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求乙在向![]() 地行驶过程中甲乙两人相距
地行驶过程中甲乙两人相距![]() 米时,甲所用时间及
米时,甲所用时间及![]() ,
,![]() 两地的距离.
两地的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com