
ЎҫМвДҝЎҝТСЦӘЛДұЯРОABCDКЗХэ·ҪРОЈ¬өгPФЪЦұПЯBCЙПЈ¬өгGФЪЦұПЯADЙПЈЁPЈ¬GІ»УлХэ·ҪРО¶ҘөгЦШәПЈ¬ЗТФЪCDөДН¬ІаЈ©Ј¬PD=PGЈ¬DFЎНPGУЪөгHЈ¬Ҫ»ЦұПЯABУЪөгFЈ¬Ҫ«ПЯ¶ОPGИЖөгPДжКұХлРэЧӘ90ЎгөГөҪПЯ¶ОPEЈ¬Б¬ҪбEFЈ®
ЈЁ1Ј©ИзНј1Ј¬өұөгPУлөгG·ЦұрФЪПЯ¶ОBCУлПЯ¶ОADЙПКұЈ®
ўЩЗлЦұҪУРҙіцПЯ¶ОDGУлPCөДКэБҝ№ШПө(І»ТӘЗуЦӨГчЈ©Ј»
ўЪЗуЦӨЈәЛДұЯРОPEFDКЗБвРОЈ»
ЈЁ2Ј©ИзНј2Ј¬өұөгPУлөгG·ЦұрФЪПЯ¶ОBCУлПЯ¶ОADөДСУіӨПЯЙПКұЈ¬ЗлІВПлЛДұЯРОPEFDКЗФхСщөДМШКвЛДұЯРОЈ¬ІўЦӨГчДгөДІВПлЈ®


Ўҫҙр°ёЎҝЈЁ1Ј©ўЩDGЈҪ2PCЈ¬АнУЙјыҪвОцЈ»ўЪјыҪвОцЈ»ЈЁ2Ј©ЛДұЯРОPEFDКЗБвРОЈ¬АнУЙјыҪвОцЈ®
ЎҫҪвОцЎҝ
ЈЁ1Ј©ўЩҪбВЫЈәDGЈҪ2PCЈ¬ИзНј1ЦРЈ¬ЧчPMЎНADУЪMЈ®Ц»ТӘЦӨГчЛДұЯРОPMDCКЗҫШРОЈ¬НЖіцPCЈҪDMЈ¬ФЩЦӨГчMGЈҪMDјҙҝЙҪвҫцОКМвЈ®
ўЪУЙЛДұЯРОPMDCКЗҫШРОөГCDЈҪPMЈ¬УЙЎчADFЎХЎчMPGЈ¬НЖіцPGЈҪPFЈ¬Ҫш¶шҝЙөГDPЈҪPFЈ¬ФЩЦӨГчDFЎОPEЈ¬НЖіцЛДұЯРОPEFDКЗЖҪРРЛДұЯРОЈ¬ФЩҪбәПPDЈҪPEјҙҝЙЦӨГчЛДұЯРОPEFDКЗБвРОЈ»
ЈЁ2Ј©ИзНј2ЦРЈ¬ЧчPMЎНADУЪMЈ®ФтЛДұЯРОCDMPКЗҫШРОЈ¬CDЈҪPMЈ¬УЙЎчADFЎХЎчMPGЈ¬НЖіцDPЈҪPGЈҪPEЈҪPFЈ¬ФЩЦӨГчDFЎОPEЈ¬НЖіцЛДұЯРОPEFDКЗЖҪРРЛДұЯРОЈ¬УЙPDЈҪPEЈ¬јҙҝЙЦӨГчЛДұЯРОPEFDКЗБвРОЈ®
ҪвЈәЈЁ1Ј©ўЩҪбВЫЈәDGЈҪ2PCЈ®
АнУЙЈәИзНј1ЦРЈ¬ЧчPMЎНADУЪMЈ®

ЎЯЛДұЯРОABCDКЗХэ·ҪРОЈ¬
ЎаЎПCЈҪЎПCDMЈҪЎПDMPЈҪ90ЎгЈ¬ADЈҪCDЈ¬
ЎаЛДұЯРОDCPMКЗҫШРОЈ¬
ЎаPCЈҪDMЈ¬
ЎЯPDЈҪPGЈ¬PMЎНDGЈ¬
ЎаMGЈҪMDЈ¬
ЎаDGЈҪ2PCЈ®
ПЯ¶ОDGУлPCөДКэБҝ№ШПөОӘDGЈҪ2PCЈ®
ўЪЎЯЛДұЯРОCDMPКЗҫШРОЈ¬
ЎаCDЈҪPMЈ¬
ЎЯADЈҪCDЈ¬
ЎаADЈҪPMЈ¬
ЎЯDFЎНPGЈ¬
ЎаЎПDAFЈҪЎПPMGЈҪЎПGHDЈҪ90ЎгЈ¬
ЎаЎПADF+ЎПAFDЈҪ90ЎгЈ¬ЎПADF +ЎПPGMЈҪ90ЎгЈ¬
ЎаЎПAFDЈҪЎПPGMЈ¬
ФЪЎчADFәНЎчMPGЦРЈ¬
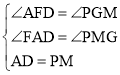 Ј¬
Ј¬
ЎаЎчADFЎХЎчGMPЈ¬
ЎаDFЈҪPG
ЎЯPGЈҪPEЈҪPDЈ¬
ЎаDPЈҪPGЈҪPEЈҪPDЈ¬
ЎЯЎПFHGЈҪЎПEPGЈҪ90ЎгЈ¬
ЎаDFЎОPEЈ¬
ЎаЛДұЯРОPEFDКЗЖҪРРЛДұЯРОЈ¬
ЎЯPDЈҪPEЈ¬
ЎаЛДұЯРОPEFDКЗБвРОЈ®
ЈЁ2Ј©ҪбВЫЈәЛДұЯРОPEFDКЗБвРОЈ®
АнУЙЈәИзНј2ЦРЈ¬ЧчPMЎНADУЪMЈ®ФтЛДұЯРОCDMPКЗҫШРОЈ¬CDЈҪPMЈ¬
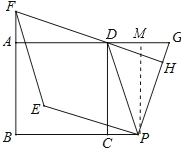
ЎЯЎПDAFЈҪЎПPMGЈҪЎПDHGЈҪ90ЎгЈ¬
ЎаЎПADF+ЎПAFDЈҪ90ЎгЈ¬ЎПG+ЎПGDHЈҪ90ЎгЈ¬
ЎЯЎПADFЈҪЎПGDHЈ¬
ЎаЎПAFDЈҪЎПGЈ¬
ЎЯADЈҪCDЈ¬CDЈҪPMЈ¬
ЎаADЈҪPMЈ¬
ФЪЎчADFәНЎчMPGЦРЈ¬
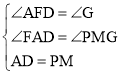 Ј¬
Ј¬
ЎаЎчADFЎХЎчMPGЈ¬
ЎаDPЈҪPGЈҪPEЈҪPDЈ¬
ЎЯЎПFHGЈҪЎПEPGЈҪ90ЎгЈ¬
ЎаDFЎОPEЈ¬
ЎаЛДұЯРОPEFDКЗЖҪРРЛДұЯРОЈ¬
ЎЯPDЈҪPEЈ¬
ЎаЛДұЯРОPEFDКЗБвРОЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬°СТ»ёцЦұҪЗИэҪЗРОACBЈЁЎПACB=90ЎгЈ©ИЖЧЕ¶ҘөгBЛіКұХлРэЧӘ60ЎгЈ¬К№өГөгCРэЧӘөҪABұЯЙПөДТ»өгDЈ¬өгAРэЧӘөҪөгEөДО»ЦГЈ®FЈ¬G·ЦұрКЗBDЈ¬BEЙПөДөгЈ¬BF=BGЈ¬СУіӨCFУлDGҪ»УЪөгHЈ®

ЈЁ1Ј©ЗуЦӨЈәCF=DGЈ»
ЈЁ2Ј©ЗуіцЎПFHGөД¶ИКэЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ABЎОCDЈ¬ADЎОBCЈ¬OEЈҪOFЈ¬ФтНјЦРИ«өИИэҪЗРОөДЧйКэКЗЈЁ Ј©

A.3ЧйB.4ЧйC.5ЧйD.6Чй
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЛДұЯРОABCDКЗБвРОЈ¬өгDөДЧшұкКЗЈЁ0Ј¬![]() Ј©Ј¬ТФөгCОӘ¶ҘөгөДЕЧОпПЯy=ax2+bx+cЗЎәГҫӯ№эxЦбЙПAЎўBБҪөгЈ®
Ј©Ј¬ТФөгCОӘ¶ҘөгөДЕЧОпПЯy=ax2+bx+cЗЎәГҫӯ№эxЦбЙПAЎўBБҪөгЈ®
ЈЁ1Ј©ЗуAЎўBЎўCИэөгөДЧшұкЈ»
ЈЁ2Ј©Зу№эAЎўBЎўCИэөгөДЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ3Ј©ИфҪ«ЙПКцЕЧОпПЯСШЖд¶ФіЖЦбПтЙПЖҪТЖәуЗЎәГ№эDөгЈ¬ЗуЖҪТЖәуЕЧОпПЯөДҪвОцКҪЈ¬ІўЦёіцЖҪТЖБЛ¶аЙЩёцөҘО»іӨ¶ИЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝН¬С§ГЗЈ¬КэС§АҙФҙУЪЙъ»оУЦ·юОсУЪЙъ»оЈ¬АыУГКэС§ЦРөДЦӘК¶ҝЙТФ°пЦъОТГЗҪвҫцРн¶аКөјКОКМв.ИзНхГчПлҪЁТ»ёці¬КРЈ¬ҫӯөчІй·ўПЦЛыјТёҪҪьУРБҪёцҙуөДҫУГсЗш![]() Ј¬
Ј¬![]() Ј¬Н¬КұУЦУРПаҪ»өДБҪМх№«В·
Ј¬Н¬КұУЦУРПаҪ»өДБҪМх№«В·![]() Ј¬
Ј¬![]() Ј¬ОӘ·ҪұгҪш»хәНҫУГсЙъ»оЈ¬НхГчПл°Сі¬КРҪЁФЪөҪБҪҫУГсЗшөДҫаАлПаөИЈ¬Н¬КұөҪБҪ№«В·ҫаАлТІПаөИөДО»ЦГЙПЈ¬»жЦЖБЛИзПВөДҫУГсЗшәН№«В·өДО»ЦГНј.ҙПГчөДДгТ»¶ЁДЬУГЛщС§өДКэС§ЦӘК¶°пЦъНхГчФЪНјЙПИ·¶Ёі¬КРөДО»ЦГЈЎЗлУГіЯ№жЧчНјИ·¶Ёі¬КРөг
Ј¬ОӘ·ҪұгҪш»хәНҫУГсЙъ»оЈ¬НхГчПл°Сі¬КРҪЁФЪөҪБҪҫУГсЗшөДҫаАлПаөИЈ¬Н¬КұөҪБҪ№«В·ҫаАлТІПаөИөДО»ЦГЙПЈ¬»жЦЖБЛИзПВөДҫУГсЗшәН№«В·өДО»ЦГНј.ҙПГчөДДгТ»¶ЁДЬУГЛщС§өДКэС§ЦӘК¶°пЦъНхГчФЪНјЙПИ·¶Ёі¬КРөДО»ЦГЈЎЗлУГіЯ№жЧчНјИ·¶Ёі¬КРөг![]() өДО»ЦГ.(ЧчНјІ»РҙЧч·ЁЈ¬ө«ТӘЗуұЈБфЧчНјәЫјЈ)
өДО»ЦГ.(ЧчНјІ»РҙЧч·ЁЈ¬ө«ТӘЗуұЈБфЧчНјәЫјЈ)
ПИҪ«КөјКОКМвЧӘ»ҜОӘКэС§ОКМвЈ¬°Сі¬КРҝҙЧчТ»ёцөг.
өг![]() өҪ
өҪ![]() Ј¬
Ј¬![]() БҪөгөДҫаАлПаөИЈ¬ёщҫЭРФЦКЈә__________________Ј¬ РиУГіЯ№жЧчіц_____________Ј»УЦөг
БҪөгөДҫаАлПаөИЈ¬ёщҫЭРФЦКЈә__________________Ј¬ РиУГіЯ№жЧчіц_____________Ј»УЦөг![]() өҪБҪПаҪ»ЦұПЯ
өҪБҪПаҪ»ЦұПЯ![]() Ј¬
Ј¬![]() өДҫаАлПаөИЈ¬ёщҫЭРФЦКЈә_________________Ј¬ РиУГіЯ№жЧчіц_______________Ј»¶шөг
өДҫаАлПаөИЈ¬ёщҫЭРФЦКЈә_________________Ј¬ РиУГіЯ№жЧчіц_______________Ј»¶шөг![]() Н¬КұВъЧгЙПКцБҪёцМхјюЈ¬ТтҙЛУҰёГКЗЛьГЗөДҪ»өг.
Н¬КұВъЧгЙПКцБҪёцМхјюЈ¬ТтҙЛУҰёГКЗЛьГЗөДҪ»өг.
ЗлН¬С§ГЗПИНкіЙ·ЦОц№эіМ(јҙМоҝХ) Ј¬ФЩЧчНјЈ»

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬°СТ»ҝйИэҪЗ°е·ЕФЪЦұҪЗЧшұкПөөЪТ»ПуПЮДЪЈ¬ЖдЦР30ЎгҪЗөД¶ҘөгAВдФЪyЦбЙПЈ¬ЦұҪЗ¶ҘөгCВдФЪxЦбөДЈЁ![]() Ј¬0Ј©ҙҰЈ¬ЎПACO=60ЎгЈ¬өгDОӘABұЯЙПЦРөгЈ¬Ҫ«ЎчABCСШxЦбПтУТЖҪТЖЈ¬өұөгAВдФЪЦұПЯy=x©Ғ3ЙПКұЈ¬ПЯ¶ОCDЙЁ№эөДГж»эОӘ_____Ј®
Ј¬0Ј©ҙҰЈ¬ЎПACO=60ЎгЈ¬өгDОӘABұЯЙПЦРөгЈ¬Ҫ«ЎчABCСШxЦбПтУТЖҪТЖЈ¬өұөгAВдФЪЦұПЯy=x©Ғ3ЙПКұЈ¬ПЯ¶ОCDЙЁ№эөДГж»эОӘ_____Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝРЎУұәНРЎББЙПЙҪУОНжЈ¬РЎУұіЛЧшАВіөЈ¬РЎББІҪРРЈ¬БҪИЛПаФјФЪЙҪ¶ҘөДАВіөЦХөг»бәП.ТСЦӘРЎББРРЧЯөҪАВіөЦХөгөДВ·іМКЗАВіөөҪЙҪ¶ҘөДПЯВ·іӨөД2ұ¶Ј¬РЎУұФЪРЎББіц·ўәу50·ЦІЕіЛЙПАВіөЈ¬АВіөөДЖҪҫщЛЩ¶ИОӘ180ГЧ/·ЦЈ¬ЙиРЎББіц·ўx·ЦәуРРЧЯөДВ·іМОӘyГЧЈ®НјЦРөДХЫПЯұнКҫРЎББФЪХыёцРРЧЯ№эіМЦРyЛжxөДұд»Ҝ№ШПө.
ЈЁ1)РЎББРРЧЯөДЧЬВ·іМКЗ_________ГЧЈ¬ЛыНҫЦРРЭПўБЛ___________·ЦЈ»
ЈЁ2Ј©·ЦұрЗуіцРЎББФЪРЭПўЗ°әНРЭПўәуЛщЧЯөДВ·іМ¶ОЙПөДІҪРРЛЩ¶ИЈ»
ЈЁ3Ј©өұРЎУұөҪҙпАВіөЦХөгКұЈ¬РЎББАлАВіөЦХөгөДВ·іМКЗ¶аЙЩЈҝ

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЛДұЯРОABCDКЗҫШРОЈ¬өгEФЪADұЯЙПЈ¬өгFФЪADөДСУіӨПЯЙПЈ¬ЗТBE=CFЈ®
ЈЁ1Ј©ЗуЦӨЈәЛДұЯРОEBCFКЗЖҪРРЛДұЯРОЈ®
ЈЁ2Ј©ИфЎПBEC=90ЎгЈ¬ЎПABE=30ЎгЈ¬AB=![]() Ј¬ЗуEDөДіӨЈ®
Ј¬ЗуEDөДіӨЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
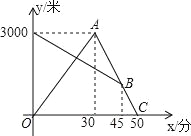
ЎҫМвДҝЎҝДіМмФзіҝЈ¬ХЕЗҝҙУјТЕЬІҪИҘМеУэ¶НБ¶Ј¬Н¬КұВиВиҙУМеУэіЎіҝБ·ҪбКш»ШјТЈ¬НҫЦРБҪИЛПаУцЈ¬ХЕЗҝЕЬөҪМеУэіЎәу·ўПЦТӘПВУкЈ¬Бўјҙ°ҙФӯВ··ө»ШЈ¬УцөҪВиВиәуБҪИЛТ»Жр»ШөҪјТЈЁХЕЗҝәНВиВиКјЦХФЪН¬Т»МхұКЦұөД№«В·ЙПРРЧЯЈ©Ј®ИзНјКЗБҪИЛАлјТөДҫаАлyЈЁГЧЈ©УлХЕЗҝіц·ўөДКұјдxЈЁ·ЦЈ©Ц®јдөДәҜКэНјПуЈ¬ёщҫЭНјПуРЕПўҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ЗуХЕЗҝ·ө»ШКұөДЛЩ¶ИЈ»
ЈЁ2Ј©ВиВиұИ°ҙФӯЛЩ·ө»ШМбЗ°¶аЙЩ·ЦЦУөҪјТЈҝ
ЈЁ3Ј©ЗлЦұҪУРҙіцХЕЗҝУлВиВиәОКұПаҫа1000ГЧЈҝ
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com