
����Ŀ��Сӱ��С����ɽ���棬Сӱ�����³���С�����У�������Լ��ɽ�����³��յ���.��֪С�����ߵ��³��յ��·�����³���ɽ������·����2����Сӱ��С��������50�ֲų����³����³���ƽ���ٶ�Ϊ180��/�֣���С������x�ֺ����ߵ�·��Ϊy�ף�ͼ�е����߱�ʾС�����������߹�����y��x�ı仯��ϵ.
��1)С�����ߵ���·����_________�ף���;����Ϣ��___________�֣�
��2���ֱ����С������Ϣǰ����Ϣ�����ߵ�·�̶��ϵIJ����ٶȣ�
��3����Сӱ�����³��յ�ʱ��С�����³��յ��·���Ƕ��٣�

���𰸡���1��3600 ��20����2��65����/�֣���55����/�֣�����3��1100���ף�.
��������
(1)����ͼ���֪С���ߵ���·�̺���;��Ϣ��ʱ�䣻
(2)����ͼ���֪��Ϣǰ����30���ӣ�1950�ף���Ϣ������30���ӣ�3600-1950�ף��ɴ˸����ٶȹ�ʽ������⼴�ɣ�
(3)������³������յ�����ʱ�䣬�Ӷ����С�����ߵ�ʱ�䣬���������������Сӱ�����³��յ�ʱ��С�����³��յ��·�� ��
(1)����ͼ���֪��С����ʻ����·��Ϊ3600m����;��Ϣʱ��Ϊ��50��30=20min��
�ʴ�Ϊ��3600��20��
(2)�۲�ͼ���֪С����Ϣǰ����30���ӣ�1950�ף�����С����Ϣǰ���ٶ�Ϊ��![]() (��/��)��
(��/��)��
С����Ϣ����ٶ�Ϊ��![]() (��/��)��
(��/��)��
��С����Ϣǰ���ٶ�Ϊ65��/�֣���Ϣ����ٶ�Ϊ55��/�֣�
(3)�³���ɽ������·��Ϊ3600��2=1800�ף�
�³������յ�����ʱ��Ϊ1800��180=10���ӣ�
Сӱ�����³��յ�ʱ��С�����ߵ�ʱ��Ϊ10+50=60���ӣ�
80��60��20(��)��
��Сӱ�����յ�ʱ��С�����³��յ��·��Ϊ��20![]() 55=1100(��)��
55=1100(��)��
�𣺵�Сӱ�����³��յ�ʱ��С�����³��յ��·����1100��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1���Ȼ�������ֵ�� ![]() �£�1+
�£�1+ ![]() ��������x=2017��
��������x=2017��
��2����֪����x2��2x+m��3=0��������ȵ�ʵ��������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���һ����11000Ԫ����ij��ƴװ�����˽������ۣ��ܿ�����һ�գ��̼�����24000Ԫ�ڶ��ι���ͬ������ˣ������������ǵ�һ�ε�2���������۹���10Ԫ��
��1������̼ҵ�һ�ι��������˶��ٸ���
��2�������л����˶�����ͬ�ı�����ۣ�Ҫ��ȫ��������ϵ������ʲ�����20%���������������أ�����ôÿ�������˵ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����κ���y=ax2+bx+c��ͼ����x�ύ��A��B���㣬����A������Ϊ����1��0������C��0��5�����������߾����㣨1��8����MΪ���Ķ��㣮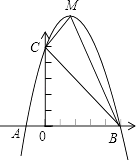
��1���������ߵĽ���ʽ��
��2�����MCB�����S��MCB ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+5��ͼ���뷴��������y= ![]() ��k��0���ڵ�һ����ͼ����A��1��n����B���㣮
��k��0���ڵ�һ����ͼ����A��1��n����B���㣮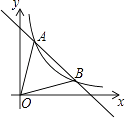
��1�����������Ľ���ʽ���B���ꣻ
��2�����AOB�������
��3���ڵ�һ�����ڣ���һ�κ���y=��x+5��ֵС�ڷ���������y= ![]() ��k��0����ֵʱ��д���Ա���x��ȡֵ��Χ��
��k��0����ֵʱ��д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ������㷨�����κ���y= ![]() +bx+c��ͼ��ʱ���г�������ı���
+bx+c��ͼ��ʱ���г�������ı���
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | ��11 | ��2 | 1 | ��2 | ��5 | �� |
���ڴ��ģ������������һ��yֵ��������������ֵ�ǣ� ��.
A����11 B����2 C��1 D����5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����š�������+��ʱ���ĵ�����һ�����ʹ�ʽ�ܵ����ڻ�ӭ���ô�ʽ���ܷ�������̷Ѻͺ�ʱ����ɣ�������̷Ѱ�xԪ/������㣬��ʱ�Ѱ�yԪ/���Ӽ��㣨�ܷ��ò���9Ԫ��9Ԫ�Ƽۣ���С����С�������øô�ʽ���У��������Ƽ۹�������ܷ��á���ʻ��������ʱ�������
ʱ�䣨���ӣ� | ���������� | ���ѣ�Ԫ�� | |
�� | 8 | 8 | 12 |
�� | 12 | 10 | 16 |
��1����x��y��ֵ��
��2�����С��Ҳ�øô�ʽ������ʻ��11�������14���ӣ���ôС���Ĵ��ܷ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A1��1��0����x��Ĵ��ߣ���ֱ��y��2x�ڵ�B1����A2���O����ֱ��A1B1�Գƣ�����A2��2��0����x��Ĵ��ߣ���ֱ��y��2x�ڵ�B2����A3���O����ֱ��A2B2�Գƣ�����A3��4��0����x��Ĵ��ߣ���ֱ��y��2x�ڵ�B3���������˹�������ȥ�����Bn������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���
��1��̽����֪����ͼ1����֪��ABC���ABD�������ȣ����ж�AB��CD��λ�ù�ϵ����˵�����ɣ�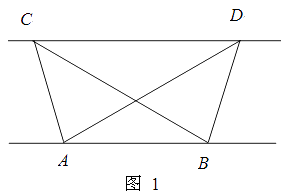
��2������Ӧ�ã��� ��ͼ2����M��N�ڷ��������� ![]() ��k��0����ͼ���ϣ�����M��ME��y�ᣬ����N��NF��x�ᣬ����ֱ�ΪE��F����֤����MN��EF��
��k��0����ͼ���ϣ�����M��ME��y�ᣬ����N��NF��x�ᣬ����ֱ�ΪE��F����֤����MN��EF�� 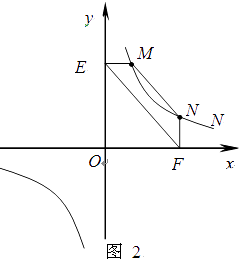
�� �����е������������䣬ֻ�ı��M��N��λ����ͼ3��ʾ�����ж� MN��EF�Ƿ�ƽ�У���˵������.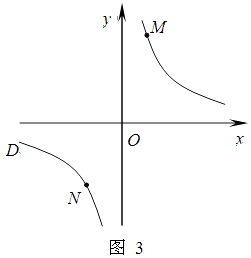
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com