
【题目】如图,一次函数y=﹣x+5的图象与反比例函数y= ![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.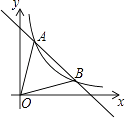
(1)求反比例函数的解析式与点B坐标;
(2)求△AOB的面积;
(3)在第一象限内,当一次函数y=﹣x+5的值小于反比例函数y= ![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
【答案】
(1)解:∵一次函数y=﹣x+5的图象过点A(1,n),
∴n=﹣1+5,解得:n=4,
∴点A的坐标为(1,4).
∵反比例函数y= ![]() (k≠0)过点A(1,4),
(k≠0)过点A(1,4),
∴k=1×4=4,
∴反比例函数的解析式为y= ![]() .
.
联立  ,解得:
,解得: ![]() 或
或 ![]() ,
,
∴点B的坐标为(4,1)
(2)解:延长AB交x轴与点C,则C(5,0),如图所示.
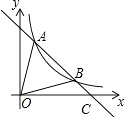
∵A(1,4),B(4,1),
∴S△AOB=S△AOC﹣S△BOC= ![]() OCyA﹣
OCyA﹣ ![]() OCyB=10﹣
OCyB=10﹣ ![]() =
= ![]()
(3)解:观察函数图象,发现:
当0<x<1或x>4时,反比例函数图象在一次函数图象上方,
∴当一次函数y=﹣x+5的值小于反比例函数y= ![]() (k≠0)的值时,x的取值范围为0<x<1或x>4
(k≠0)的值时,x的取值范围为0<x<1或x>4
【解析】(1)由一次函数y=﹣x+5的图象过点A(1,n),求出点A的坐标,得到反比例函数的解析式,求出点B的坐标;(2)直线AB交x轴与点C,得到C(5,0),求出S△AOB=S△AOC﹣S△BOC的面积;(3)观察函数图象,当0<x<1或x>4时,反比例函数图象在一次函数图象上方,得到一次函数的值小于反比例函数的值时,x的取值范围.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2﹣4ac>0;④a+b+c<0;⑤对于图象上的两点(﹣6,m )、(1,n),有m<n.其中正确信息的个数有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x-3)(x2-4x+1)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y-3)(y+1)+4 (第一步)
= y2-2y+1 (第二步)
=(y-1)2 (第三步)
=(x2-4x-1)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格。
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 |
|
|
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答。
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形 ![]() 的边长
的边长 ![]() .某一时刻,动点
.某一时刻,动点 ![]() 从
从 ![]() 点出发沿
点出发沿 ![]() 方向以
方向以 ![]() 的速度向
的速度向 ![]() 点匀速运动;同时,动点
点匀速运动;同时,动点 ![]() 从
从 ![]() 点出发沿
点出发沿 ![]() 方向以
方向以 ![]() 的速度向
的速度向 ![]() 点匀速运动,问:
点匀速运动,问: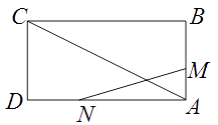
(1)经过多少时间, ![]() 的面积等于矩形
的面积等于矩形 ![]() 面积的
面积的 ![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与 ![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com