Question

16．为促进我市经济的快速发展，加快道路建设，某高速公路建设工程中需修隧道AB，如图，在山外一点C测得BC=200m，∠CAB=54°，∠CBA=30°．
（Ⅰ）∠ACB的度数为96°；
（Ⅱ）求隧道AB的长．（参考数据：tan54°=1.4，$\sqrt{3}$=1.7，结果保留整数）

Answer 1

分析 （Ⅰ）由三角形内角和定理来解答；
（Ⅱ）首先过点C作CD⊥AB于D，然后在Rt△BCD中，利用三角函数的知识，求得BD，CD的长，继而在Rt△ACD中，利用∠CAB的正切求得AD的长，继而求得答案．

解答 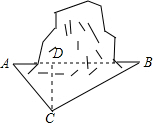解：（Ⅰ）在△ABC中，∠CAB=54°，∠CBA=30°，则∠ACB=180°-54°-30°=96°．
故答案是：96°；

（Ⅱ）过点C作CD⊥AB于D，
∵BC=200m，∠CBA=30°，
∴在Rt△BCD中，CD=$\frac{1}{2}$BC=100m，
BD=BC•cos30°=200×$\frac{\sqrt{3}}{2}$=100$\sqrt{3}$≈170（m）．
∵∠CAB=54°，
∴在Rt△ACD中，AD=$\frac{CD}{tan∠CAB}$=$\frac{CD}{tan54°}$=$\frac{100}{1.4}$≈71（m）．
∴AB=AD+BD≈170+71=241（m）．
答：隧道AB的长约为241m．

点评 此题考查了解直角三角形的应用．此题难度适中，注意掌握辅助线的作法，注意把实际问题转化为数学问题求解．