
 如图,一次函数y=ax-2(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点,且与x轴、y轴分别交于点C、D.已知tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$.
如图,一次函数y=ax-2(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点,且与x轴、y轴分别交于点C、D.已知tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$.分析 (1)先过点A作AE⊥x轴于E,构造Rt△AOE,再根据tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$,求得AE=1,OE=3,即可得出A(-3,1),进而运用待定系数法,求得一次函数和反比例函数的解析式;
(2)先点F是点D关于x轴的对称点,求得F(0,2),再根据解方程组求得B(1,-3),最后根据△ABF的面积=△ADF面积+△BDF面积,进行计算即可.
解答 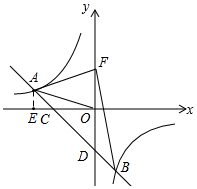 解:(1)过点A作AE⊥x轴于E,
解:(1)过点A作AE⊥x轴于E,
∵tan∠AOC=$\frac{1}{3}$,AO=$\sqrt{10}$,
∴Rt△AOE中,AE=1,OE=3,
∵点A在第二象限,
∴A(-3,1),
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象过点A,
∴k=-3×1=-3,
∴反比例函数的解析式为y=-$\frac{3}{x}$,
∵一次函数y=ax-2(a≠0)的图象过点A,
∴1=-3a-2,
解得a=-1,
∴一次函数的解析式为y=-x-2;
(2)一次函数的解析式y=-x-2中,令x=0,则y=-2,
∴D(0,-2),
∵点F是点D关于x轴的对称点,
∴F(0,2),
∴DF=2+2=4,
解方程组$\left\{\begin{array}{l}{y=-x-2}\\{y=-\frac{3}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$,
∴B(1,-3),
∵△ADF面积=$\frac{1}{2}$×DF×CE=6,
△BDF面积=$\frac{1}{2}$×DF×|xB|=2,
∴△ABF的面积=△ADF面积+△BDF面积=6+2=8.
点评 本题主要考查了反比例函数与一次函数交点问题,解决问题的关键是运用待定系数法求得一次函数和反比例函数的解析式.解题时注意:求正比例函数,只要一对x,y的值就可以;而求一次函数y=kx+b,则需要两组x,y的值.


科目:初中数学 来源: 题型:解答题
 如图,点A是第一象限内的点,坐标为(4,y),OA与x轴正半轴的夹角α的正弦角α的正弦值为$\frac{3}{5}$,求点A的坐标及α的余弦值.
如图,点A是第一象限内的点,坐标为(4,y),OA与x轴正半轴的夹角α的正弦角α的正弦值为$\frac{3}{5}$,求点A的坐标及α的余弦值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 天气 |
| 9月15日 | 晴 |
| 9月16日 | 阴 |
| 9月17日 | 阴 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
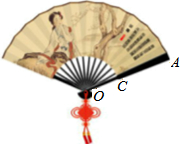 中国扇文化有着深厚的文化底蕴,是民族文化的一个组成部分,它与竹文化、佛教文化有着密切关系.历来中国被誉为制扇王国.扇子主要材料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其它棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各种千姿百态的日用工艺扇,造型优美,构造精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头合并归一而得名.如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).
中国扇文化有着深厚的文化底蕴,是民族文化的一个组成部分,它与竹文化、佛教文化有着密切关系.历来中国被誉为制扇王国.扇子主要材料是:竹、木、纸、象牙、玳瑁、翡翠、飞禽翎毛、其它棕榈叶、槟榔叶、麦杆、蒲草等也能编制成各种千姿百态的日用工艺扇,造型优美,构造精制,经能工巧匠精心镂、雕、烫、钻或名人挥毫题诗作画,使扇子艺术身价倍增.折扇,古称“聚头扇“,或称为撒扇,或折叠扇,以其收拢时能够二头合并归一而得名.如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,求出扇面的面积(用代数式表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com