
【题目】如图,矩形ABCD中,![]() ,
,![]() ,将矩形折叠,使点B与点D重合,点A的对应点为
,将矩形折叠,使点B与点D重合,点A的对应点为![]() ,折痕EF的长为________.
,折痕EF的长为________.

【答案】![]()
【解析】
过点F作FH⊥AD于H,先利用矩形的性质及轴对称的性质证明DE=DF=BF,在Rt△DCF中通过勾股定理求出DF的长,再求出HE的长,再在Rt△HFE中利用勾股定理即可求出EF的长.
解:如图,过点F作FH⊥AD于H,
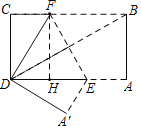
∵四边形ABCD为矩形,
∴BC∥AD,∠C=90°,DC=AB=4,四边形DCFH为矩形,
∴∠BFE=∠DEF,
由折叠可知,∠BFE=∠DFE,BF=DF,
∴∠DEF=∠DFE,
∴DE=DF=BF,
在Rt△DCF中
设DF=x,则CF=BC-BF=6-x,
∵DC2+CF2=DF2,
∴42+(6-x)2=x2,
解得,x=![]() ,
,
∴DE=DF=BF=![]() ,
,
∴CF=BC-BF=6-![]() =
=![]() ,
,
∵四边形DCFH为矩形,
∴HF=CD=4,DH=CF=![]() ,
,
∴HE=DE-DH=![]() ,
,
∴在Rt△HFE中,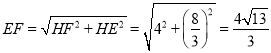
故答案为![]()


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠O=30°,点B是OM边上的一个点光源,在边ON上放一平面镜.光线BC经
过平面镜反射后,反射光线与边OM的交点记为E,则△OCE是等腰三角形的个数有( )
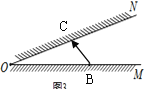
A. 1个 B. 2个 C. 3个 D. 3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图。按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入。(其中AB=9m,BC=0.5m)为标明限高,请你根据该图计算CE。(精确到0.1m)(参考数值![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从泰州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为80 km/h,B车的平均速度为A车的1.5倍,且行完全程B车所需时间比A车少40分钟.
(1)求泰州至南京的铁路里程;
(2)若两车以各自的平均速度分别从泰州、南京同时相向而行,问经过多少时间两车相距40 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A.社区板报、B.集会演讲、C.喇叭广播、D.发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:


请结合统计图表,回答下列问题:
(1)本次抽查的学生共______人,m=____________,并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式中随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
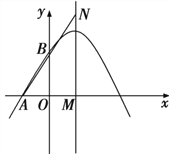
【题目】如图,抛物线![]() 过
过![]() 两点.
两点.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 为抛物线对称轴与x轴的交点,N为对称轴上一点,若
为抛物线对称轴与x轴的交点,N为对称轴上一点,若![]() ,求M到AN的距离.
,求M到AN的距离.
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 为等腰三角形?若存在,请直接写出满足条件的点
为等腰三角形?若存在,请直接写出满足条件的点
P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
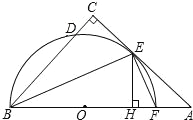
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚运用本学期的知识,设计了一个数学探究活动.如图1,数轴上的点![]() ,
,![]() 所表示的数分别为0,12.将一枚棋子放置在点
所表示的数分别为0,12.将一枚棋子放置在点![]() 处,让这枚棋子沿数轴在线段
处,让这枚棋子沿数轴在线段![]() 上往复运动(即棋子从点
上往复运动(即棋子从点![]() 出发沿数轴向右运动,当运动到点
出发沿数轴向右运动,当运动到点![]() 处,随即沿数轴向左运动,当运动到点
处,随即沿数轴向左运动,当运动到点![]() 处,随即沿数轴向右运动,如此反复).并且规定棋子按照如下的步骤运动:第1步,从点
处,随即沿数轴向右运动,如此反复).并且规定棋子按照如下的步骤运动:第1步,从点![]() 开始运动
开始运动![]() 个单位长度至点
个单位长度至点![]() 处;第2步,从点
处;第2步,从点![]() 继续运动
继续运动![]() 单位长度至点
单位长度至点![]() 处;第3步,从点
处;第3步,从点![]() 继续运动
继续运动![]() 个单位长度至点
个单位长度至点![]() 处…例如:当
处…例如:当![]() 时,点
时,点![]() 、
、![]() 、
、![]() 的位置如图2所示.
的位置如图2所示.
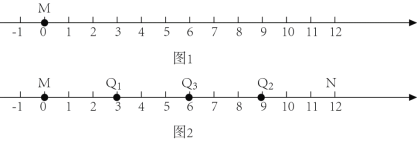
解决如下问题:
(1)如果![]() ,那么线段
,那么线段![]() ______;
______;
(2)如果![]() ,且点
,且点![]() 表示的数为3,那么
表示的数为3,那么![]() ______;
______;
(3)如果![]() ,且线段
,且线段![]() ,那么请你求出
,那么请你求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com