
【题目】如图,四边形ABCD是边长为1的正方形,且DE=![]() ,△ABF是△ADE的旋转图形
,△ABF是△ADE的旋转图形
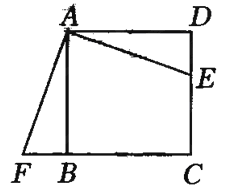
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
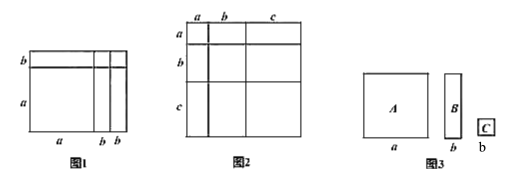
【题目】我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:
![]() 就可以用如图所示的面积关系来说明。
就可以用如图所示的面积关系来说明。
(1)请根据如图写出代数恒等式,并根据所写恒等式计算:![]()
(2)若![]() 求
求![]() 的值;
的值;
(3)现有如图中的彩色卡片:A型、B型、C型,把这些卡片不重叠不留缝隙地贴在棱长为![]() 的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AB=2,∠P=30°,求阴影部分的面积.
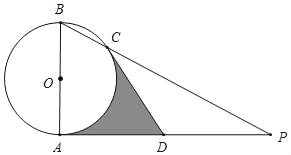
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?


把AC沿∠A的角平分线AD翻折,因为AB>AC,所以点C落在AB上的点![]() 处,即
处,即![]() ,据以上操作,易证明
,据以上操作,易证明![]() ≌
≌![]() ,所以
,所以![]() ,又因为
,又因为![]() >∠B,所以∠C>∠B.
>∠B,所以∠C>∠B.
感悟与应用:
(1)如图(a),在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;
(2)如图(b),在四边形ABCD中,AC平分∠BAD,AC=16,AD=8,DC=BC=12,
① 求证:∠B+∠D=180°;
② 求AB的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题:

(l)利用树状图(或列表)的方法表示游戏所有可能出现的结果;
(2)求甲、乙两人获胜的概率,并说明游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com