
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
【答案】(1)x;(2)x=![]() ;(3)见解析;(4)1<x<
;(3)见解析;(4)1<x<![]() .
.
【解析】试题(1)由已知条件得到∠AQP=45°,求得PQ=AP=2x,由于D为PQ中点,于是得到DQ=x;
(2)如图①,延长FE交AB于G,由题意得AP=2x,由于D为PQ中点,得到DQ=x,求得GP=2x,列方程于是得到结论;
(3)如图②,当0<x≤![]() 时,根据正方形的面积公式得到y=x2;如图③,当
时,根据正方形的面积公式得到y=x2;如图③,当![]() <x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=
<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=![]() AB=2,根据正方形和三角形面积公式得到y=﹣
AB=2,根据正方形和三角形面积公式得到y=﹣![]() x2+20x﹣8;如图④,当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到结论;
x2+20x﹣8;如图④,当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到结论;
(4)当Q与C重合时,E为BC的中点,得到x=1,当Q为BC的中点时,BQ=![]() ,得到x=
,得到x=![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,
∴∠AQP=45°,
∴PQ=AP=2x,
∵D为PQ中点,
∴DQ=x,
(2)如图①,延长FE交AB于G,由题意得AP=2x,
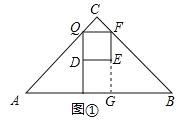
∵D为PQ中点,
∴DQ=x,
∴GP=2x,
∴2x+x+2x=4,
∴x=![]() ;
;
(3)如图②,当0<x≤![]() 时,y=S正方形DEFQ=DQ2=x2,
时,y=S正方形DEFQ=DQ2=x2,
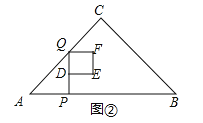
∴y=x2;
如图③,当![]() <x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=
<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=![]() AB=2,
AB=2,
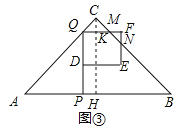
∵PQ=AP=2x,CK=2﹣2x,
∴MQ=2CK=4﹣4x,FM=x﹣(4﹣4x)=5x﹣4,
∴y=S正方形DEFQ﹣S△MNF=DQ2﹣![]() FM2,
FM2,
∴y=x2﹣![]() (5x﹣4)2=﹣
(5x﹣4)2=﹣![]() x2+20x﹣8,
x2+20x﹣8,
∴y=﹣![]() x2+20x﹣8;
x2+20x﹣8;
如图④,当1<x<2时,PQ=4﹣2x,
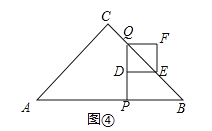
∴DQ=2﹣x,
∴y=S△DEQ=![]() DQ2,
DQ2,
∴y=![]() (2﹣x)2,
(2﹣x)2,
∴y=![]() x2﹣2x+2;
x2﹣2x+2;
(4)当Q与C重合时,E为BC的中点,
即2x=2,
∴x=1,
当Q为BC的中点时,BQ=![]() ,
,
PB=1,
∴AP=3,
∴2x=3,
∴x=![]() ,
,
∴边BC的中点落在正方形DEFQ内部时x的取值范围为:1<x<![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,∠ACB=∠ADB=90°,E为AB中点,连接DE、CE、CD.

(1)求证:DE=CE;
(2)若∠CAB=25°,∠DBA=35°,判断△DEC的形状,并说明理由;
(3)当∠CAB+∠DBA=45°时,若CD=12,取CD中点F,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
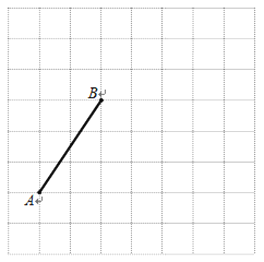
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:![]() 根据点
根据点![]() 的坐标建立坐标系,即可写出点
的坐标建立坐标系,即可写出点![]() 的坐标.
的坐标.
![]() 画出点
画出点![]() 旋转后的对应点
旋转后的对应点![]() 连接
连接![]() ,写出点
,写出点![]() 的坐标.
的坐标.
![]() 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程.
详解:(1)建立坐标系如图,
B点的坐标为![]() ;
;
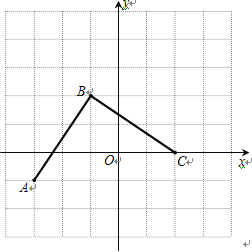
(2)线段BC如图,C点的坐标为![]()
(3)把点![]() 代入二次函数
代入二次函数![]() ,得
,得

解得:
二次函数解析为:![]()
对称轴方程为:![]()
故对称轴方程是![]()
点睛:考查图形与坐标;旋转、对称变换;待定系数法求二次函数解析式,二次函数的图象与性质.熟练掌握各个知识点是解题的关键.
【题型】解答题
【结束】
18
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(
(3)99991×99999=___________________(直接填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D. 求证:PC=PD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,且DE=![]() ,△ABF是△ADE的旋转图形
,△ABF是△ADE的旋转图形
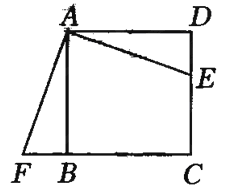
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com