
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

【答案】(1)证明见解析;(2)30°.
【解析】
由三角形的内角和可求出∠ECB=35°,根据角平分线的定义可求∠ACB=70°,进而可求出∠BAC=70°,从而结论可证;
(2)由AP是△AEC边EC上的中线可知AP=PC,从而∠PAC=∠PCA,由CE是∠ACB的平分线,可证∠PAC=∠PCA=∠PCD,从而可求出∠PAC的度数,然后求出∠BAD=60°,继而可求出∠B的值.
(1)证明:∵∠B=40°,∠AEC=75°,
∴∠ECB=∠AEC﹣∠B=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∠BAC=180°﹣∠B﹣∠ACB=180°﹣40°﹣70°=70°,
∴∠BAC=∠BCA,
∴AB=AC.
(2)∵∠BAC=90°,AP是△AEC边EC上的中线,
∴AP=PC,
∴∠PAC=∠PCA,
∵CE是∠ACB的平分线,
∴∠PAC=∠PCA=∠PCD,
∵∠ADC=90°,
∴∠PAC=∠PCA=∠PCD=90°÷3=30°,
∴∠BAD=60°,
∵∠ADB=90°,
∴∠B=90°﹣60°=30°.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】(1)如图![]() ,在等腰直角
,在等腰直角![]() 中,
中,![]() ,
,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,则
,则![]() 的面积为_______.
的面积为_______.

(2)如图![]() ,在直角
,在直角![]() 中,
中,![]() ,
,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,求
,求![]() 的面积,并说明理由.(用含
的面积,并说明理由.(用含![]() 的式子表示)
的式子表示)
(3)如图![]() ,在等腰
,在等腰![]() 中,
中,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的面积为 (用含
的面积为 (用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
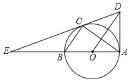
【题目】如图,AB是⊙O直径,C是半圆上一点,连接BC、AC,过点O作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=3,CE=![]() ,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).
,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
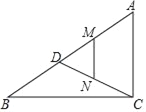
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,点D是线段AB上的动点,M、N分别是AD、CD的中点,连接MN,当点D由点A向点B运动的过程中,线段MN所扫过的区域的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的平分线,则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
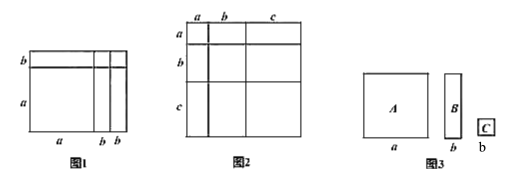
【题目】我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:
![]() 就可以用如图所示的面积关系来说明。
就可以用如图所示的面积关系来说明。
(1)请根据如图写出代数恒等式,并根据所写恒等式计算:![]()
(2)若![]() 求
求![]() 的值;
的值;
(3)现有如图中的彩色卡片:A型、B型、C型,把这些卡片不重叠不留缝隙地贴在棱长为![]() 的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
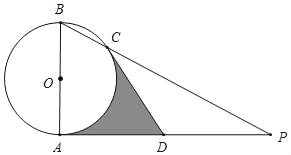
【题目】如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AB=2,∠P=30°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题:

(l)利用树状图(或列表)的方法表示游戏所有可能出现的结果;
(2)求甲、乙两人获胜的概率,并说明游戏是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com