
【题目】(1)如图![]() ,在等腰直角
,在等腰直角![]() 中,
中,![]() ,
,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,则
,则![]() 的面积为_______.
的面积为_______.

(2)如图![]() ,在直角
,在直角![]() 中,
中,![]() ,
,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,求
,求![]() 的面积,并说明理由.(用含
的面积,并说明理由.(用含![]() 的式子表示)
的式子表示)
(3)如图![]() ,在等腰
,在等腰![]() 中,
中,![]() ,将边
,将边![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的面积为 (用含
的面积为 (用含![]() 的式子表示).
的式子表示).
【答案】(1)18;(2)![]() ;理由见解析;(3)
;理由见解析;(3)![]()
【解析】
(1)首先连接AD,根据等腰直角三角形的性质得出∠CAB=∠CBA=45°,然后根据AB=BD,∠ABD=90°,得出∠BAD=∠BDA=45°,进而得出∠CBA=∠BAD,内错角相等,得出AD∥BC,进而得出△BCD的高即为AC,即可得出面积;
(2)首先过D作CB边上的高DG交CB的延长线于G,根据∠ACB=∠ABD=90°进行等角转换,得出∠ABC=∠BDG,∠A=∠DBG,即可判定△ABC≌△DBG(ASA),得出BC=DG,进而得出面积;
(3)首先作AE⊥BC于E,根据等腰三角形三线合一的性质,得出CE=BE=![]() ,依据(2)中的方法同理可得△ABE≌△BDF,得出△BCD的高即为EB,即可求得面积.
,依据(2)中的方法同理可得△ABE≌△BDF,得出△BCD的高即为EB,即可求得面积.
(1)连接AD,如图所示
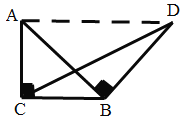
∵等腰直角![]() ,
,![]()
∴∠CAB=∠CBA=45°
又∵AB=BD,∠ABD=90°
∴∠BAD=∠BDA=45°
∴∠CBA=∠BAD
∴AD∥BC
∴△BCD的高即为AC
∴![]()
(2)过D作CB边上的高DG交CB的延长线于G,如图所示

∵∠ACB=∠ABD=90°
∴∠ABC+∠A=∠ABC+∠DBG=∠DBG+∠BDG
∴∠ABC=∠BDG,∠A=∠DBG
又∵AB=BD
∴△ABC≌△DBG(ASA)
∴BC=DG
∴![]()
(3)作AE⊥BC于E,DF⊥CB,交CB的延长线于F,如图所示

∵等腰![]() 中,
中,![]() ,
,
∴CE=BE=![]()
由(2),同理可得,△ABE≌△BDF
△BCD的高即为EB
![]()


科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经决定购买甲型设备不少于3台,预算购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为240吨,乙型设备每月的产量为180吨.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠ACB=∠ADB=90°,E为AB中点,连接DE、CE、CD.

(1)求证:DE=CE;
(2)若∠CAB=25°,∠DBA=35°,判断△DEC的形状,并说明理由;
(3)当∠CAB+∠DBA=45°时,若CD=12,取CD中点F,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】符合下列条件之一的四边形不一定是菱形的是( )
A. 四条边相等
B. 两组邻边分别相等
C. 对角线相互垂直平分
D. 两条对角线分别平分一组对角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌化妆品商店有![]() 、
、![]() 、
、![]() 三种型号的化妆品,今年国庆节期间采用组合打折销售,销售时采用了三种组合的方式进行销售,甲种组合是:
三种型号的化妆品,今年国庆节期间采用组合打折销售,销售时采用了三种组合的方式进行销售,甲种组合是:![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种;乙种组合是:
种;乙种组合是:![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种;丙种组合是:
种;丙种组合是:![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种,
种,![]() 盒
盒![]() 种.如果组合销售打折后A种每盒售价为
种.如果组合销售打折后A种每盒售价为![]() 元,
元,![]() 种每盒售价为
种每盒售价为![]() 元,
元,![]() 种每盒售价为
种每盒售价为![]() 元.国庆节当天,商店采用三种组合搭配的方式进行销售后共得销售额为
元.国庆节当天,商店采用三种组合搭配的方式进行销售后共得销售额为![]() 元,其中
元,其中![]() 种的销售额为
种的销售额为![]() 元,那么
元,那么![]() 种化妆品的销售额是______.
种化妆品的销售额是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.求证:四边形ABEF为菱形;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com