
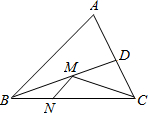
 在锐角三角形ABC中,BC=
在锐角三角形ABC中,BC= ,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是________.
,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN的最小值是________. ,∠ABC=45°,BD平分∠ABC可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.
,∠ABC=45°,BD平分∠ABC可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.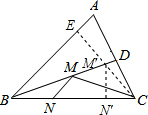 解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,则CE即为CM+MN的最小值,
解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,则CE即为CM+MN的最小值, ,∠ABC=45°,BD平分∠ABC,
,∠ABC=45°,BD平分∠ABC, ×
× =4.
=4.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com