
 在平面坐标系中,正方形ABCD的位置如图,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交于x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2016个正方形A2015B2015C2015C2014的面积为5×($\frac{9}{4}$)2015.
在平面坐标系中,正方形ABCD的位置如图,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交于x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2016个正方形A2015B2015C2015C2014的面积为5×($\frac{9}{4}$)2015. 分析 根据点A、D的坐标求出OA、OD的长,然后利用勾股定理列式求出AD,再求出△AOD和△A1BA相似,根据相似三角形对应边成比例列式求出A1B,从而求出第二个正方形的边长A1C=A1B1,同理求出第三个正方形的边长A2C1=A2B2,根据规律求出第2015个正方形的边长,再根据正方形的面积公式列式计算即可得解.
解答 解:∵点A(1,0),点D(0,2),
∴OA=1,OD=2,
∴AD=$\sqrt{O{D}^{2}+O{A}^{2}}$=$\sqrt{5}$,
∵∠ADO+∠DAO=180°-90°=90°,
∠DAO+∠BAA1=180°-90°=90°,
∴∠ADO=∠BAA1,
又∵∠AOD=∠ABA1=90°,
∴△AOD∽△A1BA,
∴$\frac{OD}{AB}$=$\frac{OA}{{A}_{1}B}$,
∴A1B=$\frac{OA•AB}{OD}$=$\frac{\sqrt{5}}{2}$,
∴第二个正方形的边长:A1C=A1B1=$\sqrt{5}$+$\frac{\sqrt{5}}{2}$=$\frac{3\sqrt{5}}{2}$,
同理A2B1=$\frac{1}{2}$×$\frac{3\sqrt{5}}{2}$=$\frac{3\sqrt{5}}{4}$,
∴第三个正方形的边长:A2C1=A2B2=$\frac{3\sqrt{5}}{2}$+$\frac{3\sqrt{5}}{4}$=$\frac{9\sqrt{5}}{4}$=($\frac{3}{2}$)2×$\sqrt{5}$,
第四个正方形的边长:$\frac{9\sqrt{5}}{4}$+$\frac{9\sqrt{5}}{8}$=$\frac{27\sqrt{5}}{8}$=($\frac{3}{2}$)3×$\sqrt{5}$…,
第2015个正方形的边长:($\frac{3}{2}$)2015×$\sqrt{5}$,
∴第2015个正方形的面积为[($\frac{3}{2}$)2015×$\sqrt{5}$]2=5×($\frac{9}{4}$)2015.
故答案为:5×($\frac{9}{4}$)2015.
点评 此题考查了正方形的性质,相似三角形的判定与性质,依次求出正方形的边长是解题的关键.


科目:初中数学 来源: 题型:填空题
 探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是β-α.
探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠BOC=β,则∠DCO的度数是β-α.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{2}$ | C. | 10$\sqrt{5}$ | D. | 5$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
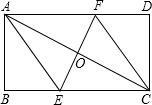 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com