
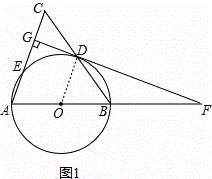
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=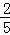 ,求CG的长.
,求CG的长.
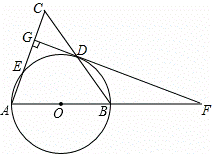
(1)证明:如图1,连接OD,
∵AB=AC,
∴∠C=∠ABC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODG=∠DGC,
∵DG⊥AC,
∴∠DGC=90°,
∴∠ODG=90°,
∴OD⊥FG,
∵ OD是⊙O的半径,
OD是⊙O的半径,
∴直线FG是⊙O的切线.
(2)解:如图2,
∵AB=AC=10,AB是⊙O的直径,
∴OA=OD=10÷2=5,
由(1),可得
OD⊥FG,OD∥AC,
∴∠ODF=90°,∠DOF=∠A,
在△ODF和△AGF中,

∴△ODF∽△AGF,
∴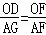 ,
,
∵cosA=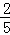 ,
,
∴cos∠DOF=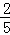 ,
,
∴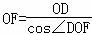 =
=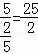 ,
,
∴AF=AO+OF=5 ,
,
∴ ,
,
解得AG=7,
∴CG=AC﹣AG=10﹣7=3,
即CG的长是3.



 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )
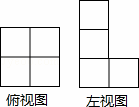
A. 5或6或7 B. 6或7 C. 6或7或8 D. 7或8或9
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为 .
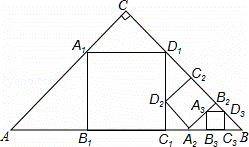
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中真命题是( )
(A)两边分别对应相等且有一角为30º的两个等腰三角形全等
(B)两边和其中一边的对角分别对应相等的两个三角形全等
(C)两个锐角分别对应相等的两个直角三角形全等
(D)两角和一边分别对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在□ABCD中, ∠B=110°,延长AD至F,
延长CD至E,连接EF,则∠E+∠F的值为( )
(A)110° (B)30° (C)50° (D)70°
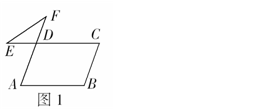 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com