
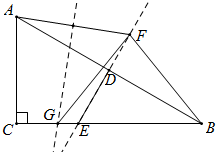
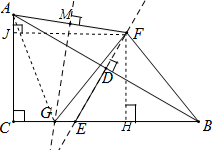
 已知如图,在Rt△ABC中,∠C=90°,∠B=30°,D为AB的中点,E为BC上一点,且DE⊥AB,垂足为D.点F在ED的延长线上,连接BF、AF,作AF的垂直平分线交EC于点G,连接FG,请探究BF与FG之间的数量关系,并证明你的结论.
已知如图,在Rt△ABC中,∠C=90°,∠B=30°,D为AB的中点,E为BC上一点,且DE⊥AB,垂足为D.点F在ED的延长线上,连接BF、AF,作AF的垂直平分线交EC于点G,连接FG,请探究BF与FG之间的数量关系,并证明你的结论.| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
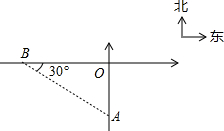 如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?
如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 6 |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com