如图.四个二次函数的图像中.分别对应的是①y = ax2,②y = bx2,③y = cx2, ④y = dx2．则a.b.c.d的大小关系为A．a>b>c>dB．a>b>d>cC．b>a>c>dD．b>a>d>c 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，四个二次函数的图像中，分别对应的是①y = ax²；②y = bx²；③y = cx²； ④y = dx²．
则a、b、c、d的大小关系为（）

A．a>b>c>d

B．a>b>d>c

C．b>a>c>d

D．b>a>d>c

解：由二次函数

的性质知，
（1）抛物线

的开口大小由

决定．

越大，抛物线的开口越窄；

越小，抛物线的开口越宽．
（2）抛物线

的开口方向由a决定．
当a＞0时，开口向上，抛物线（除顶点外）都在x轴上方；
当a＜0时，开口向下，抛物线（除顶点外）都在x轴下方．
根据以上结论知：a＞b＞0＞c＞d．
故选A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：不详 题型：解答题

已知抛物线y＝ax²＋bx＋c（a＞0）的图象经过点B（14,0）和C（0，－8），对称轴为x＝4．
（1）求该抛物线的解析式；
（2）点D在线段AB上且AD＝AC，若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动，同时另一动点Q以某一速度从C出发沿线段CB匀速运动，问是否存在某一时刻，使线段PQ被直线CD垂直平分？若存在，请求出此时的时间t（秒）和点Q的运动速度；若不存在，请说明理由；
（3）在（2）的结论下，直线x＝1上是否存在点M使△MPQ为等腰三角形？若存在，请求出所有点M的坐标，若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源：不详 题型：填空题

将抛物线y=x²-2x向上平移3个单位，再向右平移4个单位得到的抛物线解析式为 .

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

烟花厂为热烈庆祝“十一国庆”，特别设计制作一种新型礼炮，这种礼炮的升空高度

与飞行时间

的关系式是

，礼炮点火升空后会在最高点处引爆，则这种礼炮能上升的最大高度为（　　）

A．91米

B．90米

C．81米

D．80米

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

小明从下边的二次函数

图像中，观察得出了下面的五条信息：①

，②

，③函数的最小值为-3，④当

时，

，⑤当

，

。你认为其中正确的个数为

A．2

B．3

C．4 　

D．5

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

已知二次函数y=x²-5x-6．
(1)求此函数图象的顶点A和其与x轴的交点B和C的坐标；
(2)求△ABC的面积．

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

已知点(3，

₎,(4，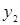

), (5，

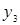)在函数y=2x²+8x+7的图象上,则y₁,y₂,y₃的大小关系是( )

A．y₁>y₂>y₃

B．y₂> y₁> y₃

C．y₂>y₃> y₁

D．y₃> y₂> y₁

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

已知抛物线

与y轴交于C点，与x轴交于A、B两点，点A的坐标是（－1，0），O是坐标原点，且

．
（1）求抛物线的函数表达式；
（2）直接写出直线BC的函数表达式；
（3）如图1，D为y轴的负半轴上的一点，且OD=2，以OD为边作正方形ODEF.将正方形ODEF
以每秒1个单位的速度沿x轴的正方向移动，在运动过程中，设正方形ODEF与△OBC重叠部分的面积为s，运动的时间为t秒（0＜t≤2）.
求：①s与t之间的函数关系式； ②在运动过程中，s是否存在最大值？如果存在，直接写出这个最大值；如果不存在，请说明理由．
（4）如图2，点P（1，k）在直线BC上，点M在x轴上，点N在抛物线上，是否存在以A、M、
N、P为顶点的平行四边形？若存在，请直接写出M点坐标；若不存在，请说明理由.