
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

【答案】(1)平行;(2)见解析;(3)![]() .
.
【解析】
(1)根据三角形中位线定理得出DE∥BC,DE=![]() BC,FG∥BC,FG=
BC,FG∥BC,FG=![]() BC,那么DE∥FG,DE=FG,利用有一组对边平行且相等的四边形是平行四边形即可得出四边形DEFG是平行四边形;
BC,那么DE∥FG,DE=FG,利用有一组对边平行且相等的四边形是平行四边形即可得出四边形DEFG是平行四边形;
(2)先由矩形的性质得出OD=OE=OF=OG.再根据重心的性质得到OB=2OD,OC=2OE,等量代换得出OB=OC.利用SAS证明△BOE≌△COD,得出BE=CD,然后根据中点的定义即可证明AB=AC;
(3)连接AO并延长交BC于点M,先由三角形中线的性质得出M为BC的中点,由(2)得出AB=AC,根据等腰三角形三线合一的性质得出AM⊥BC,再由三角形中位线定理及三角形重心的性质得出BC=2FG=4,AM=![]() AO=6,由勾股定理求出AB=2
AO=6,由勾股定理求出AB=2![]() ,进而得到△ABC的周长.
,进而得到△ABC的周长.
(1)解:∵△ABC的中线BD,CE交于点O,
∴DE∥BC,DE=![]() BC,
BC,
∵F,G分别是BO,CO的中点,
∴FG∥BC,FG=![]() BC,
BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形.
故答案为平行;
(2)证明:∵四边形DEFG是矩形,
∴OD=OE=OF=OG.
∵△ABC的中线BD,CE交于点O,
∴点O是△ABC的重心,
∴OB=2OD,OC=2OE,
∴OB=OC.
在△BOE与△COD中,
 ,
,
∴△BOE≌△COD(SAS),
∴BE=CD,
∵E、D分别是AB、AC中点,
∴AB=AC;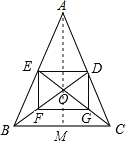
(3)解:连接AO并延长交BC于点M.
∵三角形的三条中线相交于同一点,△ABC的中线BD、CE交于点O,
∴M为BC的中点,
∵四边形DEFG是正方形,
由(2)可知,AB=AC,
∴AM⊥BC.
∵正方形DEFG边长为2,F,G分别是BO,CO的中点,
∴BC=2FG=4,BM=MC=![]() BC=2,AO=2EF=4,
BC=2,AO=2EF=4,
∴AM=![]() AO=6,
AO=6,
∴AB=![]() =
=![]() =2
=2![]() ,
,
∴△ABC的周长=AB+AC+BC=4![]() +4.
+4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
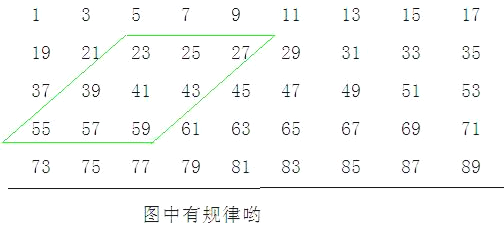
【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
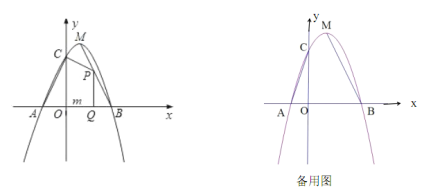
【题目】如图,已知二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,顶点为
,顶点为![]() .
.
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,求出点
为直角三角形?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
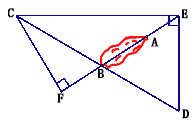
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=![]() .
.
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).
(1)观察一个等比列数1,![]() ,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以 ![]()
请根据以上的解答过程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示an;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+an.
查看答案和解析>>
科目:初中数学 来源: 题型:
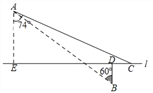
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM= ;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第 秒时,∠COM与∠CON互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )

A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com