
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM= ;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第 秒时,∠COM与∠CON互补.
【答案】(1)90°,OM平分∠CON;(2)∠AOM=∠CON,详见解析;(3)15或60.
【解析】
(1)由旋转得∠BOM=90°,求出∠COM=45°=∠MON即可得到OM平分∠CON.
(2)先求出∠AOC=45°,得到∠CON+∠AON=45°,再由∠MON=45°得到∠AOM+∠AON=45°,即可证得∠AOM=∠CON;
(3)分三种情况讨论:①当OM在∠BOC内部时,②当OM在∠BOC外部,ON在∠BOC内部时,③当ON在∠BOC外部时,分别求出时间t的值.
(1)由题意得,∠BOM=90°,∠MON=45°,
OM平分∠CON,理由如下:
∵∠BOC=135°,
∴∠COM=∠BOC-∠BOM=45°,
∴∠COM=∠MON
∴OM平分∠CON;
(2)∠AOM=∠CON,理由如下:
∵∠AOC=180°-∠BOC=45°,
∴∠CON+∠AON=45°,
∵∠MON=45°,
∴∠AOM+∠AON=45°,
∴∠AOM=∠CON;
(3)设运动t秒(0![]() ),
),
①当OM在∠BOC内部时,∠COM=![]() ,
,
∴2![]() +45=180,
+45=180,
得t=15;
②当OM在∠BOC外部,ON在∠BOC内部时,
∠COM+∠CON=45°,不合题意,舍去;
③当ON在∠BOC外部时,∠CON=![]() ,
,
∴2![]() =180,
=180,
得t=60,
∴当旋转到第15或60秒时,∠COM与∠CON互补


科目:初中数学 来源: 题型:
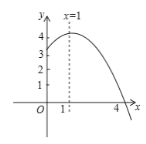
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )

A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 9cm
cm D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随时用的共享单车。某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费。具体收费标准如下:

同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:

(1)写出a、b的值。
(2)已知该校有5100名师生,且A品牌共享单车投放该校一天的费用为5800元。试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 的面积为 63,D 是 BC 上的一点,且 BD:BC=2:3, DE∥AC 交 AB 于点 E,延长 DE 到 F,使 FE:ED=2:1.连结 CF 交 AB 点于 G.
(1)求△BDE 的面积;
(2)求 ![]() 的值;
的值;
(3)求△ACG 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:数学课上,老师出示了这祥一个问题:
如图,在正方形ABCD中,点F在AB上,点E在BC延长线上。且AF=CE,连接EF,过点D作DH⊥FE于点H,连接CH并延长交BD于点0,∠BFE=75°.求![]() 的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法:
小柏:“通过观察和度量,发现点H是线段EF的中点”。
小吉:“∠BFE=75°,说明图形中隐含着特殊角”;
小亮:“通过观察和度量,发现CO⊥BD”;
小刚:“题目中的条件是连接CH并延长交BD于点O,所以CO平分∠BCD不是己知条件。不能由三线合一得到CO⊥BD”;
小杰:“利用中点作辅助线,直接或通过三角形全等,就能证出CO⊥BD,从而得到结论”;……;
老师:“延长DH交BC于点G,若刪除∠BFB=75°,保留原题其余条件,取AD中点M,连接MH,如果给出AB,MH的值。那么可以求出GE的长度”.
请回答:(1)证明FH=EH;
(2)求![]() 的值;
的值;
(3)若AB=4.MH=![]() ,则GE的长度为_____________.
,则GE的长度为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com