
【题目】如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,
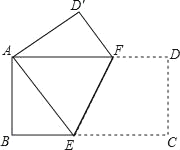
求 (1)AE的长.(2)折痕EF的长.
【答案】(1)5;(2)2![]() .
.
【解析】
(1)根据折叠的性质得到AE=CE,根据勾股定理即可得到结论
(2)先过点F作FG⊥BC于G.利用勾股定理可求出AE,再利用翻折变换的知识,可得到AE=CE,∠AEF=∠CEF,再利用平行线可得∠AEF=∠AFE,故有AE=AF.求出EG,再次使用勾股定理可求出EF的长.
(1)∵将长方形纸片ABCD折叠,使C点与A点重合,
∴AE=CE,
∴BE=BC-CE=BC-AE=8-AE,
∵∠B=90°,
∴AB2+BE2=AE2,
即42+(8-AE)2=AE2,
∴AE=5;
(2)过点F作FG⊥BC于G,
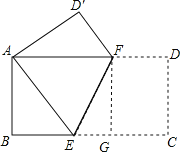
∵EF是直角梯形AECD的折痕,
∴AE=CE,∠AEF=∠CEF,
又∵AD∥BC,
∴∠CEF=∠AFE,
∵∠CEF=∠AEF,
∴∠AEF=∠AFE,
∴AE=AF,
在Rt△ABE中,
设BE=x,AB=4,AE=CE=8-x.x2+42=(8-x)2,
解得x=3,
在Rt△FEG中,EG=BG-BE=AF-BE=AE-BE=5-3=2,FG=4,
∴EF=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).
(1)观察一个等比列数1,![]() ,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以 ![]()
请根据以上的解答过程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示an;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+an.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
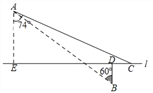
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角板的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角板绕着点O逆时针旋转90°,如图2所示,此时∠BOM= ;在图2中,OM是否平分∠CON?请说明理由;
(2)接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒4.5°的速度沿逆时针方向旋转一周,在旋转的过程中,当旋转到第 秒时,∠COM与∠CON互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用无刻度的直尺和圆规作出符合要求的图形.(注:不要求写作法,但保留作图痕迹)
(1)如图,已知线段AB,作一个△ABC,使得∠ACB=90°;(只需画一个即可)
(2)如图,已知线段MN,作一个△MPN,使得∠MPN=90°且sinM=![]() .(只需画一个即可)
.(只需画一个即可)

(1) (2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com